çoklayıcı (multiplexer)

yazan: Şadi Evren ŞEKER

Çok sayıdaki girişin tek bir giriş üzerinden taşınmasıdır. Amaç çok sayıdaki girişin (örneğin 4 giriş) tek bir çıkışa düşürülmesidir. Çalışma mantığı, anlık olarak tek bir girişi çıkışa vermek şeklindedir. Yani 4 girişten sadece bir tanesi çıkış ile kısa devre halindedir, diğer girişler ise ihmal edilir. Hangi girişin çıkışa verileceğini belirlemek için bir seçme işlemi yapılması gerekmektedir. Bu seçme işlemini yapan bitlere seçici bit(select bit) adı verilmektedir.
Örneğin 4 girişi olan bir devre için (Girişler a,b,c ve d isminde olsun) 2 adet seçici bit gerekmektedir çünü 4 bit ancak 2 bit ile adreslenebilir (2 üzeri 2) bu durumu gösteren temsili tablo aşağıda verilmiştir:

S1 S2 Ç
-- -- -
0 0 a
0 1 b
1 0 c
1 1 d

yukarıdaki tablonun çalıştığı devrenin görüntüsü aşağıda verilmiştir.

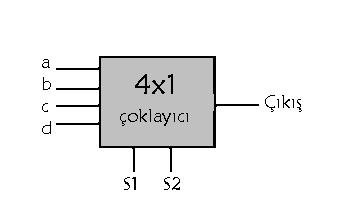
Yukarıdaki şeması verilen devrenin girişlerinden hangisini çıkış ile bağlanacağına seçici bitler karar verirler. Bu devrenin tasarımı aşağıda verilmiştir:

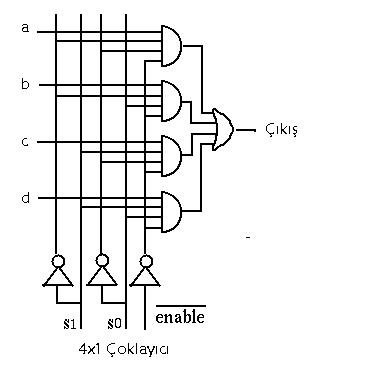
Yukarıda tanımı verilen özellik kullanılarak devre tasarımında kısaltmaya gidilebilir. Buna göre karnaugh haritasında verilen her hücre tasarımın sonucunda bir girişin bağlanması ile yapılmaktadır. Bu özellik kullanılarak bir tam toplayıcıyı, kod çözücü devre yardımı ile tasarlayalım:
Öncelikle tam toplayıcı devrenin çalışmasını hatırlayalım:

tam toplayıcı devrenin doğruluk çizelgesini hatırlayalım (3 bitlik giriş için 2 bit çıkışı olan ve girişlerin sayısal değerlerinin toplandığı devre idi):

A B C E T
- - - - -
0 0 0 0 0
0 0 1 0 1
0 1 0 0 1
0 1 1 1 0
1 0 0 0 1
1 0 1 1 0
1 1 0 1 0
1 1 1 1 1

dolayısıyla yukarıda A B ve C girişlerinin toplam değerleri T ve E bitlerinde verilmiştir.

bu doğruluk çizelgesinin karnaugh haritası aşağıda verilmiştir:

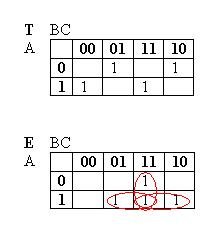
Şimdi bu karnaugh haritasının her sütunu için geçerli olan terimleri bulalım:

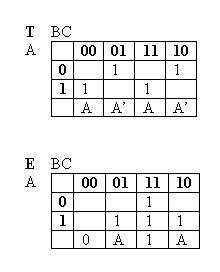
yukarıdaki tabloda, bir tam toplayicinin karnaugh haritasının üzerinde sütun bazlı olarak işlem yapılmıştır. Buna göre her sütunda (yain BC ikili ihtimali için) çıkan sonuç en alt satırda gösterilmiştir. Örneğin E biti için, BC ikilisi 11 olduğunda sonuç her zaman 1 çıkmaktadır (A bitinin sonuca bir etkisi yoktur) benzer şekilde yine E biti için BC ikilisi 0 olduğunda sonuç her zaman 0 olmaktadır (yine A bitinin sonuca bir etkisi yoktur) örneğin E biti için BC ikilis 01 olduğunda sonuç A bitine bağlıdır. Şayet A biti 1 ise sonuç 1 , A biti 0 ise sonuç 0 çıkmaktadır. Bu durumda da BC ikilisinin 01 olduğu durum için sonuç A’dır denilebilir.
O halde yukarıda verilen bu özelliklerden faydalanarak bir çoklayıcı (multiplexer) devresi ile tam toplayıcı tasarlayalım.
Bu işlemden önce dikkat edilmesi gereken bir husu, karnaugh haritalarında sütun numaraları yazılırken 00, 01, 11, 10 sıralaması ile gitmesidir. Oysaki çoklayıcı devrenin doğruluk çizelgesine dikkat edilirse sıralama 00, 01, 10, 11 şeklinde gitmektedir. Bu yüzden karnough haritasındaki son iki sütun çoklayıcı devrede yer değiştirmektedir. Okuyucu buna dikkat etmelidir.


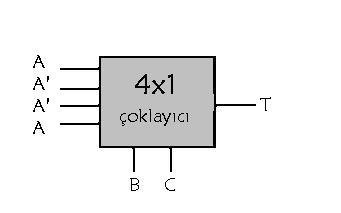
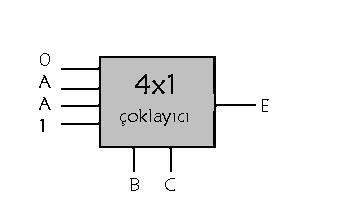
Yukarıdaki iki ayrı devrede iki ayrı çıkış değeri için çözüm yapılmıştır. Buna göre kod çözücü devre veya “ve” ve “veya” kapıları ile tasarlanan bir tam toplayıcı ile aynı işi yapan yukarıdaki devrede çoklayıcının bize sağlamış olduğu avantaj kullanılarak daha az elemanla tasarım yapılmıştır.

Çoklayıcı devreler günümüzde kullanılan pekçok devrenin temelinde bulunmaktadır. Örneğin ağ iletişiminde kullanılan HUB cihazının tasarımı basit bir multiplexerdır.