kod çözücü (decoder)

yazan: Şadi Evren ŞEKER

mantıksal devre tasrımının önemli parçalarından birisi olan kod çözücülerin çalışma mantığı giriş bitlerinin farklı bacaklara dağılmasıdır. Yani örneğin 2 girişli bir kod çözücünün 4 farklı çıkışı olur (2 üzeri 2) ve her çıkış sadece bir giriş ihtimali için çalışır. Daha basit anlatmak gerekirse aşağıdaki doğruluk çizelgesini inceleyelim:

A B a b c d
- - - - - -
0 0 1 0 0 0
0 1 0 1 0 0
1 0 0 0 1 0
1 1 0 0 0 1

yukarıdaki doğruluk çizelgesinde A ve B girişleri için 4 farklı çıkış değeri (a b c ve d) verilmiştir. Dikkat edilirse giriş değerlerinin alabileceği her ihtimal için farklı bir çıkış değeri 1 olmuş geri kalanlar 0 olmuştur.
Bu durumda kod çözücülerin ana amacı farklı girişlerin mantıksal “ve” işlemini almaktır. Yani yukarıdaki çizelgede her satırda farklı bir ihtimalin “ve” sonucu görülmektedir. Bu durum aşağıdaki tabloda gösterilmiştir:

A B a b c d
- - - - - -
0 0 A'B' -> a
0 1 A'B -> b
1 0 AB' -> c
1 1 AB -> d

yukarıdaki tabloda her satırda mantıksal olarak farklı bir ihtimal gösterilmiş ve sonucun hangi çıkış bacağında görüldüğü verilmiştir. Buna göre 2x4lük bir kod çözücünün a bacağı her zaman A’B’ önermesini verir. Bir kod çözücünün kapılar ile tasarımı aşağıdaki şekildedir.

Bu özellik kullanılarak devre tasarımında kısaltmaya gidilebilir. Çünkü klasik yaklaşımda karnaugh haritası ile çizilen devrelerde bir “ve” kapısı grubu bir de “veya” kapısı grubu bulunmaktadır (önce ve kapısında eşleşen girişler daha sonra veya kapısı ile toplanmaktadır bkz. tam toplaycı veya yarı toplayıcı) Bu yaklaşımındaki “ve” kapı grubunu kod çözücü ile kaldırarak sadece “veya” kapı grupları ile kod çözücünün çıkış bacaklarını birbirine bağlamak mümkündür. Çünkü yukraıdaki örnekte de görüleceği üzere girişlerin tamamının bütün muhtemel “ve” kapısı sonuçları kod çözücü ile bulunabilmektedir.

Örnek olarak bir tam toplayıcı devrenin kod çözücü ile tasarımı aşağıda verilmiştir:

tam toplayıcı devrenin doğruluk çizelgesini hatırlayalım (3 bitlik giriş için 2 bit çıkışı olan ve girişlerin sayısal değerlerinin toplandığı devre idi):

A B C E T
- - - - -
0 0 0 0 0
0 0 1 0 1
0 1 0 0 1
0 1 1 1 0
1 0 0 0 1
1 0 1 1 0
1 1 0 1 0
1 1 1 1 1

dolayısıyla yukarıda A B ve C girişlerinin toplam değerleri T ve E bitlerinde verilmiştir.
bu doğruluk çizelgesinin karnaugh haritası aşağıda verilmiştir:

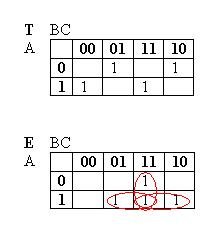
şimdi yukarıdaki haritaya ve doğruluk çizelgesine bakıldığında görülür ki aslında doğruluk çizelgesinin her satırı kod çözücünün farklı bir bacağıdır. Bu durumda tam toplayıcı devre aşağıdaki şekilde de tasarlanabilir:

Yukarıdaki devrede S, T bitine ve C ise E bitine karşılık gelmektedir. {bu devreyi çizip orjinal resim konulacak}