Yazan: Şadi Evren ŞEKER
Asgarai tarama ağacı, ağırlıklık bir ağda (weighted graph, yani her düğümü birbirine bağlayan yolların maliyeti (ağırlığı) olması durumu), bütün düğümleri dolaşan en kısa yolu verir. Örneğim aşağıdaki grafikte bütün düğümlere uğrayan en kısa yol işaretlenmiştir:
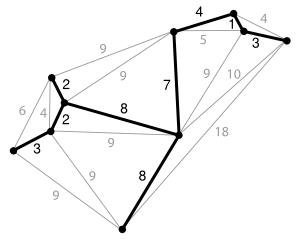
asgari tarama ağacını veren en meşhur algoritmalar:
Kruskal Algoritması
Prims Algoritması
Dijkstra Algoritması (Asgari tarama ağacının benzeri olarak bir arama algorimtası örneği)
en küçük yayılma problemi lingo çözümü:
İnceleyeceğiniz çoğu kaynaktaki karar modellerini lingoya aktarmada başarısız olursunuz çünkü en küçük yayılmada karar modeline düğümlerin döngü oluşturarak kopmalar oluşturmasını engelleyecek ekstra kısıtlar gerektirir bunu engelleyecek yapıyı vereceğim modelde aştım sizde ödevinizde gerekli yerleri değiştirerek kullanabilirsiniz zaten sadece parametre değerlerini ve sayısını değiştirmeniz gerektir büyük olasılıkla
model:
title örten agac;
sets:
dugum/1..6/;
ayrit(dugum,dugum):a,x;
endsets
min=@sum(ayrit:a*x);
@for(dugum(j)|j#ne#1:@sum(dugum(i)|i#ne#j:x(i,j))>=1);
@for(dugum(i)|i#ne#6:@sum(dugum(j)|j#ne#i:x(i,j))>=0);
@for(dugum(i):@for(dugum(j)|i#ne#j:x(i,j)+x(j,i)<=1));
@for(ayrit|a#ne#0:@bin(x));
data:
a=0 15 14 35 32 25
15 0 20 23 22 25
14 20 0 30 26 21
35 23 30 0 13 22
32 22 26 13 0 18
25 25 21 22 18 0;
enddata
end
Selam a.
-Yönsüz grafta MSP’nin en kolay yolu nedir?