Yazan : Şadi Evren ŞEKER
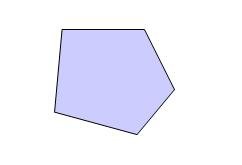
Bir düzlemde (2 boyutlu), çok sayıdaki (n adet) noktanın belirlediği kapalı alanın adıdır. Örneğin aşağıdaki bir çokgen resmedilmiştir:
Bu şekildeki her köşe bir noktadır ve koordinatlarının bilinmesi yukarıdaki şekli çizmek için yeterlidir. Yukarıdaki çokgenin ayrıca bir özelliği de dışbükey (concave) olmasıdır.
Örneğin yukarıdaki ikinci çokgen tasvirinde ise ilkinden farklı olarak mütekavvis (iç bükey, convex) yapıdaki bir çokgen resmedilmiştir.
Dolayısıyla bir çokgenin yukarıdaki gibi köşelerini belirten birer vertex (nirengi , üç boyutlu nokta) ve aynı zamanda her kenarı belirten birer vektör (yöney) ile gösterilmesi mümkündür.
Bu vektörler (yöney) bir çokgenin içbükey (mütekavvis) veya dışbükey olup olmadığını anlamak için kullanılabilir. Buna göre şayet yöneylerden birisi kendi doğrultusunda veya eksi doğrultusunda başka bir yöneyi keserse bu durumda şekil mğtekavvistir denilebilir. Örneğin aşağıdaki şekilde böyle bir yöney bulunmaktadır:
Görüldüğü üzere E2 yöneyi E4 yöneyini kesmektedir.
Çokgenleri bilgisayarlar üzerinde ifade edebilmek için çeşitli tablolardan istifade edilebilir. Örneğin aşağıdaki çokgenin tabloları yine tasvirin altında verilmiştir:


Yukarıda da görüldüğü üzere çokgen 2 yüzeyden (Surface) oluşmakta olup, çokgenin toplam 6 kenarı ve 5 noktası bulunmaktadır.
Bilindiği üzere bir çokgen 2 boyutludur ve 2 boyutlu bir nesnenin ön ve arka yüzleri bulunmaktadır. Buna göre bir noktanın çokgenin dışında, önünde veya arkasında olduğu aşağıdaki şekilde belirlenir:

Yukarıdaki resimde de tasvir edildiği üzere bir nokta bir çokgenin önünde veya arkasında bulunabilir. Buna karar vermek için aşağıdaki matematiksel bağlantılardan faydalanılır:
A.x + B.y + C.z + D = 0 ise çokgenimizin üzerinde
A.x + B.y + C.z + D < 0 ise çokgenin arkasında
A.x + B.y + C.z + D > 0 ise çokgenin önünde demektir
Yukarıdaki örnekte bir noktanın, çokgenin neresinde bulunduğu gösterilmiştir ancak bir de çokgenin ön ve arka yüzlerine karar verilmesi sorunu bulunmaktadır. Bu sorunun çözümü için normal yöneyinden (normal vector) faydalanılır:

yukarıdaki resimde de tasvir edildiği üzere çokgeni teşkil eden yöneylerin bileşkesi alınmış ve normal yöneyi bulunmuştur. (elektronikteki manyetik akımın bulunması için kullanılan sağ el kuralına benzetilebilir). Bu işlemin sayısal karşılığı:
N = (v2-v1) x (v3-v1)
N.P = -D




Peki biz bu convex poligonları dışbukey parçalara ayıran kodları nasıl yazacaz?
merhaba hocam.
gelişigüzel çizilmiş x1,y1,x2 ve y2 lerden oluşan çizgi koordinatlarını(çizgiler kapalı poligon oluşturuyor.) birbirini izliyecek şekilde nasıl sıralıyabiliriz.
Sıralama işleminiz poligonu dolaşacak şekilde olmalı sanırım. Burada sıralama işlemini yapma şansınız ne yazık ki bulunmuyor.
Örneğin yukarıdaki şekilde bulunan poligonu ele alalım. Burada sıralamanın v1, v2, v3, v4, v5 şeklinde yapıldığını görüyoruz ancak aynı nokta koordinatları ile pek ala v1, v2, v4, v3, v5 poligonu da çizilebilirdi. Dolayısıyla nokta koordinatları bize poligon hakkında bilgi vermek için yetersizdir.
Ancak vektörel olarak sıralayabilirsiniz. Yani yine yukarıda gösterilen poligon için vektörler elimizde bulunuyorsa bu vektörlerin yönlerinden istifade ederek bir sıralamadan bahsedilebilir. Bu durumda her noktadan başlayan vektörden hemen sonra, bu vektörün uzayda kestiği diğer nokta (veya diğer vektörün başlangıcı) gelir.
başarılar
Merhabalar,
Sanırım concave ve convex isimlerini tam tersi yazdınız,