Yazan : Tuğçe Doğan
RC5 şifreleme algoritması modern şifreleme algoritmaları sınıfında yer almaktadır. 1994 yılında MIT profesörlerinden Ronald L. Rivest tarafından yazılmıştır. Bir çok donanım ile birlikte çalışabilmesi, nerdeyse tüm mikroişlemcilerde bulunan ilkel matematik işlemlerini kullanıyor olması kullanım açısından avantaj sağlamaktadır. RC5, 16 – 32 ve 64 bitli kelime uzunlukları ile çalışabilmektedir. DES, IDEA gibi geleneksel şifreleme algoritmalarında sabit olan anahtar boyutu ve döngü sayısı RC5 algoritmasında değişken olarak alınabilir. Böylece, yüksek anahtar boyutu ve fazla döngü sayısı ile uzun çalışma zamanı fakat kırılması neredeyse imkansız şifreler; düşük anahtar boyutu ve az döngü sayısı ile kısa çalışma zamanı ve bununla beraber daha güçsüz şifreler arasında seçim yapılabilme olanağını sağlar. Bellek gereksiniminin de düşüklüğü ile cep telefonlarından süper bilgisayarlara kadar her yerde çalışabilir bir algoritmadır.
RC5 Algoritmasının genel çalışma prensibi
Parametreler
w : kelime uzunluğu. Her kelime u = (w/8) 8-bit byte içerir. RC5 ikilik kelime bloklarını şifreler: düz metin ve şifreli metin 2w bit uzunluğundadır. (16, 32 ve 64)
r : döngü sayısı. Aynı zamanda genişletilmiş anahtar tablosu S, t = 2(r+1) kelime içerir.
(0 – 255)
b : anahtardaki byte uzunluğu. (0 – 255)
RC5 algortmasını şu şekilde parametreler halinde gösterebiliriz; RC5 – w/ r/ b.
Örnek olarak RC5 – 32/12/10 şeklindeki bir gösterim bize; 32 bit kelime uzunluğunun, 16 döngünün ve 18 byte (80 bit) anahtarımızın olduğu bilgilerini vermektedir. Anahtar uzunluğundan ise 2(16+1) işlemi ile 34 kelimelik bir anahtar tablosu oluşturabileceğimiz bilgisini üretebilmekteyiz.
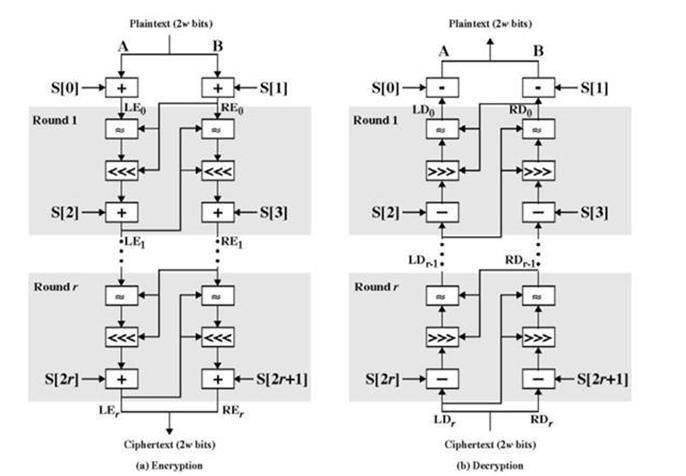
Fig. 2. Şifreleme ve çözümleme
Şifreleme
Giriş bloğunun iki w-bit şeklinde geldiğini, bunlarının A – B olduğunu ve anahtar bloğunun üretilmiş olup S[0…t-1] serisinin tamamlandığını farz edelim.
A = A + S[0];
B = B + S[1];
for i = 1 to r do
A = ((A  B) <<< B) + S[2*i];
B) <<< B) + S[2*i];
B = ((B  A) <<< A) + S[2*i+1];
A) <<< A) + S[2*i+1];
İşlemin çıktısı şifrelenmiş A ve B dir.
Çözümleme
Şifrelenmiş metin ters işlemler ile kolayca düz metine dönüşebilmektedir.
for i = r downto 1 do B = ((B – S[2*i+1] >>> A)A; A = ((A – S[2*i] >>> B )
B;
B = B – S[1]; A = A – S[0];
Analiz
RC5 algoritması oluşturulurken sistemin bir takım özellikler kazanması sağlanmıştır. Bunları şu şekilde sıralayabiliriz;
- Simetrik blok şifreleme sistemidir.
- Yazılım veya donanım ile uyumludur.
- Hızlıdır.
- İşlemlerde, farklı kelime uzunluklarına kolay adaptasyon sağlamaktadır.
- Değişken döngü sayısına sahiptir.
- Değişken anahtar uzunluğuna sahiptir.
- Kullanımı basittir.
- Kaynak kullanımı azdır.
Uygun parametreler girildiğinde yüksek güvenlik sağlamaktadır. [2]
RC5 hem yazılım hem donanım ile uyumlu, parametrelerden oluşan bir algoritmadır. Döngü sayısı, blok sayısı ve anahtar uzunluğu değişkendir. Bu özellik şifreleme sistemine esneklik, performans artışı ve yüksek güvenlik sağlamaktadır. Algoritmanın bir diğer önemli özelliği ise basitliğidir. Şifreleme 3 işleme dayalıdır; ekleme, XOR işlemi ve döngü. Yalnızca 3 işlem olması algoritmanın uygulama ve analiz kolaylığı kazanmasını sağlar. Ayrıca şifrelemede veri bağımlı döngüler kullanılması diferansiyel ve lineer şifrelerin çözülmesini önlemektedir. [3]
RC5 Algoritmasında Anahtar Üretimi
RC5 Algoritması’nın 3 temel bileşeni vardır. Bunlar; anahtar genişletilmesi algoritması, şifreleme algoritması ve çözümleme algoritmasıdır. Şifreleme ve çözümleme algoritmaları bölüm 1.2. RC5 Algoritmasının Genel Çalışma Prensibi’nde incelenmiş idi. Anahtar genişletilmesinde ise; kullanıcının girdiği anahtar K ile anahtar dizisi olan S’in t = 2 x (r+1) denklemine göre random binary kelimeler üretilmesi esas alınmaktadır. Algoritma iki sihirli değişken ve 3 algoritmik parçadan oluşmaktadır.
Sihirli sabitlerin tanımlanması
Anahtar üretim algoritması Pw ve Qw olmak üzere iki adet sabit kullanmaktadır. Bu sabitler keyfi w üretimi için aşağıdaki şekilde kullanılmaktadır:
Pw = Odd ((e–2)2w)
Qw = Odd ((Ø–2)2w)
e = 2,718281828459… (doğal algoritmasına dayanmakta)
Ø = 1,618033988749… (altın oran)
W’nun 16, 32 ve 64 olması durumunda aşağıdaki sabitler üretilir.
P16 = 1011011111100001 = b7e1
Q16 = 1001111000110111 = 9e37
P32 = 10110111111000010101000101100011 = b7e15163
Q32 = 10011110001101110111100110111001 = 9e3779b9
P64 = 1011011111100001010100010110001010001010111011010010101001101011 = b7e151628aed2a6b
Q64 = 1001111000110111011110011011100101111111010010100111110000010101 = 9e3779b97f4a7c15
Anahtarın byte’tan kelimeye çevrilmesi
İkinci aşama, üretilen gizli anahtar dizisi olan K[0..b-1] dizisinin L[0..c-1] içerisine kopyalanmasıdır. Kopyalama ve kopyalanan her kelimenin L içerisine yerleştirilmesi için birbirini takip eden u anahtar bitleri kullanılır.
c = [max (b, 1)/u] for i = b – 1 downto 0 L [i/u] = (L [i/u] <<< 8) + K[i]
S dizisinin tanımlanması
Üçüncü aşama, Pw kullanılarak S dizisinin ilk elemanının oluşturulması ve 1’den t-1’e kadar S dizisinin bir sonraki elemanını, S dizisinin o anki elemanına Qw eklenmesi ile bulunması prensibine dayanmaktadır.
S [0] = Pw; for i = 1 to t –1 ve S[i] = S [i–1] + Qw
Gizli anahtar ile karışım
Son aşama, kullanıcının gizli anahtarı ile diğer 3 aşamada oluşturulan S ve L dizilerinin birleştirilmesidir. S ve L dizilerinin uzunluklarının farklı olmasından dolayı işlem 3 kez uygulanmaktadır.
i = j = 0 do 3*max (t, c) times: S[i] = (S[i] + reg1 + reg2) <<<3 reg1 = S[i] L[j] = (L[j] + reg1 + reg2) <<< (reg1 + reg2) reg2 = L[j] i = (i +1) mod t j = (j + 1) mod c
Kriptoanaliz
Parametre seçimi RC5 algoritması için önemli ve öncelikli konudur. Her parametrenin algoritma içerisinde kullanılması uygun değildir. Örneğin döngü 0 olduğunda şifreleme olmayacağı gibi, 1 olduğunda da kolaylıkla kırılabilen bir şifreleme meydana gelmekte ve anahtar uzunluğu 0 olduğunda hiç güvenlik sunulmamaktadır. Diğer yandan seçilen maksimum değerler de oldukça önemlidir. Maksimum değerin büyüklüğü şifrelenecek olan metne gereğinden fazla güvenlik uygulanmasına neden olabilmektedir. Bu da hızdan ve dolayısıyla zamandan kayıp anlamına gelmektedir. Bir çok uygulama için hız önemli bir konudur. Bu yüzden özellikle döngü sayısındaki seçime dikkat edilmelidir.
RC5 gibi blok şifreleme algoritmalarının gücü söz konusu olduğunda algoritmada kullanılan S kutuları, döngü sayısı, anahtarların XOR işlemine sokulması, blok uzunluğu, anahtarın uzunluğu ve özelliği büyük önem taşımaktadır. [4]
RC5 algoritmasına uygulanabilecek saldırı yöntemlerini şu şekilde sıralayabiliriz;
– Ayrıntılı anahtar araması
– İstatistiksel test
– Lineer kriptoanaliz
– Diferansiyel kriptoanaliz
– Zamanlana saldırısı [5]
Ayrıntılı anahtar araması; kaba kuvvet saldırısı olarak ta bilinmektedir. Saldırı, olası tüm anahtarların denenmesi esasına dayanmaktadır. Anahtar n bitli ise, 2ⁿ adet olası durum bulunmaktadır.
İstatistiksel test; blok şifrelerin istatistiksel komşuluklarının analizinde kullanılabilmektedir.
Lineer kriptoanaliz; 1993 yılında Matsui tarafından teorik bir saldırı olarak keşfedilmiştir. Şifreli metin bitleri ile açık metin bitleri arasındarc4 yüksek olasılıkta lineer ifadelerin meydana gelme avantajını kullanan bir saldırı yöntemidir. Bunun yolu da S kutularından geçer. Saldırganın algoritmayı bildiği (Kerchoffs kuralı) ve belli sayıda açık metin ve şifreli metinlere sahip olduğu varsayılır. S kutularının büyüklüğü, aktif S kutularının (lineer ifade içinde olan) sayısının artışı ve lineer sapması (1/2 den + veya -) küçük S kutularının tasarımı lineer kriptoanalizin uygulanmasını engelleyici faktörlerdir.
Diferansiyel kriptoanaliz; 1991 yılında Biham tarafından keşfedilmiştir. Lineer kriptoanalize benzemektedir. Farkı seçilmiş açık metin saldırısı olmasıdır. Saldırı şu şekilde açıklanabilir. Elimizde açık metin/şifreli metin çiftleri (x1, x2, y1, y2) olsun ve Δx = x1  x2 sabit şekilde seçilmiş olsun. Saldırgan bir çok sayıda bu açık metin/şifreli metin çiftlerini üretir ve Δx farkına karşılık algoritmadan yüksek olasılıkta meydana gelen Δu (son döngüdeki S kutusundan önceki durum bitleri) farkını bulduktan sonra her açık/şifreli metin çiftleri için olası anahtar değerlerini dener ve Δu farkını tutması durumunda sayaç değerini o anahtar değeri için 1 arttırır. Yüksek olasılığı yakalayan anahtar değeri aranan anahtar olmuş olur. Bu saldırı da S kutularının diferansiyel kriptoanalize karşı güçlü olmasını, algoritmanın gücü için, gerekli kılar.
x2 sabit şekilde seçilmiş olsun. Saldırgan bir çok sayıda bu açık metin/şifreli metin çiftlerini üretir ve Δx farkına karşılık algoritmadan yüksek olasılıkta meydana gelen Δu (son döngüdeki S kutusundan önceki durum bitleri) farkını bulduktan sonra her açık/şifreli metin çiftleri için olası anahtar değerlerini dener ve Δu farkını tutması durumunda sayaç değerini o anahtar değeri için 1 arttırır. Yüksek olasılığı yakalayan anahtar değeri aranan anahtar olmuş olur. Bu saldırı da S kutularının diferansiyel kriptoanalize karşı güçlü olmasını, algoritmanın gücü için, gerekli kılar.
Aşağıdaki grafikte lineer ve diferansiyel kriptoanaliz sonuçları r sayıda döngü üzerinden incelenmektedir. Lineer kriptoanaliz 1995 yılında Kaliski ve Yin tarafından; diferansiyel kriptoanaliz ise 1996 yılında Knudsen ve Meier tarafından RC5 algoritması üzerine uygulanmıştır. Mavi renk lineer, pembe renk ise diferansiyel kriptoanalizi temsil etmektedir.

Fig. 3. Lineer ve diferansiyel kriptoanaliz
Aşağıdaki tabloda döngü sayısının artışı ile birlikte algoritma güvenliğinin nasıl arttığı lineer ve diferansiyel kriptoanaliz karşılaştırılarak gösterilmektedir.

Fig. 4. Döngü sayısı – saldırı yöntemi ilişkisi
RC5’in patent sahibi RCA Security, şifreleme algoritmasının kırılması için 10.000$ ödül koymuştur, ancak Mayıs 2007 tarihi ile yarışmalar iptal edilmiştir. Yalnızca distributed.net şifrelemeyi kırma çalışmalarına devam etmiştir. [1]
Aşağıda ilgili siteden alınmış 3.05.2009 tarihli veriler yer almaktadır. [6]
| Aranacak toplam blok sayısı: | 1,099,511,627,776 |
| Test edilen blok toplamı: | 6,637,941,002 |
| Kapsamlı oran: | 33 Blocks/sec |
| Aranacak toplam anahtar sayısı: | 4,722,366,482,869,646,000,000 |
| Test edilen toplam anahtar sayısı: | 28,509,739,516,367,470,000 |
| Kapsamlı oran: | 140,894,038,000 Keys/sec |
| Tamamlanan yüzde: | 0.604% |
| Çalışma zamanı: | 2,342 days |
Test
Build.alchar.org sitesinde 16 Şubat 2009 tarihinde yapılmış olan RC5 – 32 testinin sonuçları şu şekildedir [7]
Host information
Host : rctest-32 – Red Hat Enterprise Linux Server release 5.3 (Tikanga)
Kernel : Linux 2.6.29 – rc5 i386
Package : systemtap_snapshot (0.8/0.137-2.6.29_rc5-snapshot)
Timestamp : 2009/02/16 04:06:30 – 2009/02/16 13:40:26
Yapı durumu

Fig. 5. Yapı
Test durumu

Fig. 6. Durum
Son olarak RC5 algoritmasının performans testleri ve DES – RC4 algoritmaları ile karşılaştırılmaları şu şekildedir [8]
90 MHz Pentium 200 MHz DEC Alpha
DES Key Setup 17 MicroSeconds 16 MicroSeconds
RC4 Key Setup 57 MicroSeconds 138 MicroSeconds
RC5 Key Setup 48 MicroSeconds 26 MicroSeconds
DES Encrypt 8.0 MegaBits/Sec 10.6 MegaBits/Sec
RC4 Encrypt 65.6 MegaBits/Sec 34.4 MegaBits/Sec
RC5 Encrypt 26.3 MegaBits/Sec 24.5 MegaBits/Sec
Sonuç
Günümüzde blok şifreleme algoritmaları, şifrelemenin gerektiği bir çok alanda kullanılmaktadırlar. Dolayısıyla bu algoritmaların gücü güvenlik açısından çok önemlidir. RC5 şifreleme algoritmasının önemi; kullanım esnekliği, hızı, değişken anahtar ve döngü yapısı göz önüne alındığında açıkça görülmektedir. Yapılan saldırılara karşı dayanıklılığında parametrelerinin değişkenliğine oldukça işlevseldir. Yukarıdaki veriler bu çerçevede göz önüne alındığında, işlemin yeterince hızlanması için binlerce bilgisayarın daha katılması, ya da işlemcilerin çok daha hızlanması gerektiği açıkça gözükmektedir. Zira an itibari ile 2.342 gündür çalışan bir projenin sadece %0.604’ünün bitmiş olması RC5 şifrelemesinin ne kadar güçlü olduğunu göstermektedir. Günümüzün güçlü modern şifreleme algoritmalarından birini projemde inceleyerek hem bir algoritmaya güçlü denilebilmesi için gerekli olan kıstasların neler olduğunu, hem de RC5 algoritmasının tasarlanırken ne gibi aşamalardan geçtiğini görmüş oldum.
