IDEA (Uluslar arası şifreleme algoritması)

Yazan : Melda Gürsoy

Kriptografi, gizlilik, kimlik denetimi, bütünlük gibi bilgi güvenliği kavramlarını sağlamak için çalışan matematiksel yöntemler bütünüdür. Bu yöntemler, bir bilginin iletimi esnasında karşılaşılabilecek aktif ya da pasif ataklardan bilgiyi -dolayısıyla bilgi ile beraber bilginin göndericisi ve alıcısını da- koruma amacı güderler.

Bir başka deyişle kriptografi, okunabilir durumdaki bir bilginin istenmeyen taraflarca okunamayacak bir hale dönüştürülmesinde kullanılan tekniklerin tümü olarak da gösterilir.

İdea şifrelemesinin kullanımı ve önemi

Açılımı “International Data Encryption Algorithm” olan IDEA 1990’da Xuejia Lai ve James Massey tarafından bulunmuştur. 1991 yılında tasarlanmış bir blok şifreleme algoritmasıdır. Bu algoritmaya DES yerine üretilen PES’in geliştirilmiş hali denebilir. Aynı zamanda Ascom tech adlı firmanın tescilli algoritmasıdır. IDEA algoritması PGP adlı program ile kullanılarak popüler bir hal almıştır. Bilinen en güçlü algoritmalardandır. İlk öncelerini PES adıyla anılan bu algoritma geçirdiği revizyonlar ertesinde şu andaki halini almıştır. İsviçre, Zürih’de geliştirilmiştir. Patenti Ascom Systec Ltd isimli bir firmaya aittir. Ancak ticari olmayan amaçlar için lisans ücreti talep edilmemektedir. PGP’nin temelini oluşturan 2 ana algoritmadan birisidir.

Çalışması

128 bitlik bir anahtar ile 52 adet 16 bitlik alt anahtarlar kullanılarak şifreleme işlemi gerçekleştirilmekdir. Şifrelenecek olan 64 bitlik metin 16 bitlik 4 eş parçaya bölünür .8 adımda yardımcı anahtarlar kulanılarak çarpma, toplama ve xor gibi matematiksel işlemler yardımıyla şifreleme işlemi gerçekleştirilir.

Fiig. 1. Detaylar: 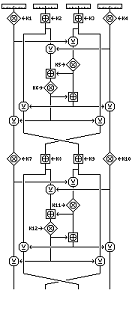Overview: Fig. 1. Genel Bakış: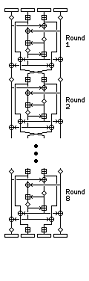

Kısaca özetlemek gerekirse ; 64-bit bloklar üzerinde 128-bit anahtar kullanan bir simetrik anahtar metodudur. IDEA patentli bir algoritmadır. RSA Laboratories tarafından geliştirilen RC5 algoritması değişken-uzunluklu anahtarlar ile çalışır. İhracat kısıtlamaları yüzünden farklı anahtar uzunluklarına ihtiyaç duyan uygulamalar için oldukça uygundur.

Analiz

IDEA 64 bitlik bloklar üzerinde 128 bit anahtar kullanılan bir simetrik anahtar metodudur. 52 adet 16 bitlik yardımcı anahtar bulunmaktadır ve IDEA algoritması çeşitli matematiksel işlemlerin karışımından oluşmaktadır. Gerçekleşen işlemler mod 65536 da ve işaretsiz bildirimde kullanılmaktadır.

Yardımcı anahtar52 tane anahtarın oluşturulmasında kullanılan 8 adetlik anahtarın kaydırılarak oluşturulması bir dezavantaj olarak yorumlanmaktadır. Buna rağmen matematiksel olarak herhangi bir eksiklik görülmemiştir. Bu algoritmanın avantaj ve dezavantajlarını toparlamak istersek ;

Avantajları

•	Algoritmalar hızlıdır
•	Algoritmaların donanımla gerçeklenmesi kolaydır

•	“Gizlilik” güvenlik hizmetini yerine getirir

Dezavantajları

•	Ölçeklenebilir değil
•	Emniyetli anahtar dağıtımı zor

•	“Bütünlük” ve “Kimlik Doğrulama” güvenlik hizmetlerini gerçeklemek zor

Yöntem ve alternatifleri

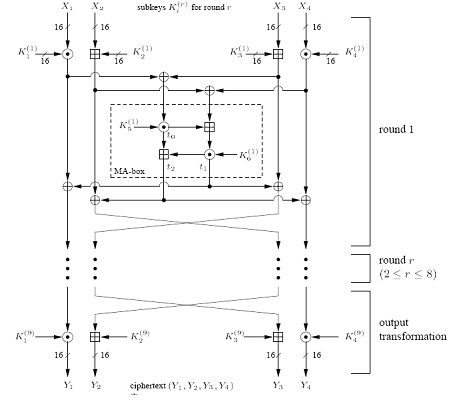
128 bitlik anahtar 16 bitlik 8 tane anahtar şeklinde parçalanır. Bu parçalanan anahtarlardan ilk 8 tanesi anahtar olarak belirlenip, 128 bitlik kısım kaydırılır ve 8 tane yeni anahtar meydana gelir. Uygulanan bu işlemler 52 anahtar olana kadar devam eder.

Şifrelenecek olan metin in dört parçaya böldüğümüzden bahsetmiştik.Bu parçaların birincisi ile birinci anahtar çarpım işlemine, ikincisi ile ikinci anahtar toplama işlemine, üçüncüsü ile üçüncü anahtar toplama işlemine ve dördüncüsü ile dördüncü anahtar çarpım işlemine tabi tutulur.

Bu böldüğümüz metnin parçalarına p1, p2, p3 ve p4 diyelim. Yardımcı anahtarları da s1,s2..s52 olduğunu düşünelim. Aşağıda metin ile yardımcı anahtarların nasıl şifreleme işlemlerine tabii tutulduğu gösterilmektedir.

p1 x s1 –> d1 p1 x s1 -> d1

p2 + s2 –> d2 p2 + s2 -> d2

p3 + s3 –> d3 p3 + s3 -> d3

p4 x s4 –> d4 p4 x s4 -> D4

d1 XOR d3 –> d5 d1 d3 XOR -> d5

d2 XOR d4 –> d6 d2 D4 XOR -> D6

d5 x s5 –> d7 d5 x S5 -> d7

d6 + d7 –> d8 D6 + d7 -> d8

d8 x s6 –> d9 d8 x S6 -> D9

d7 + d9 –> d10 d7 + D9 -> d10

d1 XOR d9 –> d11 d1 D9 XOR -> D11

d3 XOR d9 –> d12 D3 D9 XOR -> D12

d2 XOR d10 –> d13 d2 d10 XOR -> d13

d4 XOR d10 –> d14 D4 d10 XOR -> d14

Kısaca açıklamak gerekirse

1) Çarpma ve ilk alt anahtarı X1.
2) ikinci alt anahtarını X2 ekleyin.
3) ve üçüncü alt anahtarını X3 ekleyin.
4) Çarpma X4 ve dördüncü alt anahtarı.
5) adım (1) ve sonuçları XOR (3).
6) (2) ve sonuçları XOR (4).
7) Çarpma beşinci alt anahtarı ile adım (5) sonuçları.
8) adım (6) ve (7) sonuçlarına ekleyin.
9) Çarpma adım (8) altıncı alt anahtarı ile sonuçları.
10) adım (7) ve (9) sonuçlarına ekleyin.
11) adım (1) ve (9) sonuçlarına XOR.
12) adım (3) ve (9) sonuçlarına XOR.
13) adım (2) ve (10) sonuçları XOR.
14) adım (4) ve (10) sonuçları XOR.

Sekizinci tur sonra, son bir çıkış dönüşümü:
(1) Çarpma ve ilk alt anahtarı X1.
(2), ikinci alt anahtarını X2 ekleyin.
(3) ve üçüncü alt anahtarını X3 ekleyin.
(4) Çarpma X4 ve dördüncü alt anahtarı.


Round	Encryption Subkeys	Decryption Subkeys

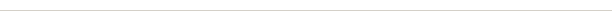1st	Z₁⁽¹⁾ Z₂⁽¹⁾ Z₃⁽¹⁾ Z₄⁽¹⁾ Z₅⁽¹⁾ Z₆⁽¹⁾	Z₁^{(9) – 1} –Z₂⁽⁹⁾ –Z₃⁽⁹⁾ Z₄^{(9) – 1} Z₅⁽⁸⁾ Z₆⁽⁸⁾
2nd	Z₁⁽²⁾ Z₂⁽²⁾ Z₃⁽²⁾ Z₄⁽²⁾ Z₅⁽²⁾ Z₆⁽²⁾	Z₁^{(8) – 1} –Z₃⁽⁸⁾ –Z₂⁽⁸⁾ Z₄^{(8) – 1} Z₅⁽⁷⁾ Z₆⁽⁷⁾
3rd	Z₁⁽³⁾ Z₂⁽³⁾ Z₃⁽³⁾ Z₄⁽³⁾ Z₅⁽³⁾ Z₆⁽³⁾	Z₁^{(7) – 1} –Z₃⁽⁷⁾ –Z₂⁽⁷⁾ Z₄^{(7) – 1} Z₅⁽⁶⁾ Z₆⁽⁶⁾
4th	Z₁⁽⁴⁾ Z₂⁽⁴⁾ Z₃⁽⁴⁾ Z₄⁽⁴⁾ Z₅⁽⁴⁾ Z₆⁽⁴⁾	Z₁^{(6) – 1} –Z₃⁽⁶⁾ –Z₂⁽⁶⁾ Z₄^{(6) – 1} Z₅⁽⁵⁾ Z₆⁽⁵⁾
5th	Z₁⁽⁵⁾ Z₂⁽⁵⁾ Z₃⁽⁵⁾ Z₄⁽⁵⁾ Z₅⁽⁵⁾ Z₆⁽⁵⁾	Z₁^{(5) – 1} –Z₃⁽⁵⁾ –Z₂⁽⁵⁾ Z₄^{(5) – 1} Z₅⁵⁽⁴⁾ Z₆⁽⁴⁾
6th	Z₁⁽⁶⁾ Z₂⁽⁶⁾ Z₃⁽⁶⁾ Z₄⁽⁶⁾ Z₅⁽⁶⁾ Z₆⁽⁶⁾	Z₁^{(4) – 1} –Z₃⁽⁴⁾ –Z₂⁽⁴⁾ Z₄^{(4) – 1} Z₅⁽³⁾ Z₆⁽³⁾
7th	Z₁⁽⁷⁾ Z₂⁽⁷⁾ Z₃⁽⁷⁾ Z₄⁽⁷⁾ Z₅⁽⁷⁾ Z₆⁽⁷⁾	Z₁^{(3) – 1} –Z₃⁽³⁾ –Z₂⁽³⁾ Z₄^{(3) – 1} Z₅⁽²⁾ Z₆⁽²⁾
8th	Z₁⁽⁸⁾ Z₂⁽⁸⁾ Z₃⁽⁸⁾ Z₄⁽⁸⁾ Z₅⁽⁸⁾ Z₆⁽⁸⁾	Z₁^{(2) – 1} –Z₃⁽²⁾ –Z₂⁽²⁾ Z₄^{(2) – 1} Z₅⁽¹⁾ Z₆⁽¹⁾
Output	Z₁⁽⁹⁾ Z₂⁽⁹⁾ Z₃⁽⁹⁾ Z₄⁽⁹⁾	Z₁^{(1) – 1} –Z₂⁽¹⁾ –Z₃⁽¹⁾ Z₄^{(1) – 1}

Şifrelenecek olan metnin birinci parçası ile üçüncü parçası ve ikinci parçası ile dördüncü parçası XOR işlemi uygulanır ve böylece yeni değerlerimiz olur. Meydana gelen sonuçlarla bir sonraki anahtar önce çarpım sonra toplama, daha sonra çarpım ve en son yine toplama işlemi uygulanır.

8 döngüden, 4 çıktı bloğuna e1 ,e2 ,e3 ve e4 dersek, aşağıda şekil üzerinde şifreli metin bloklarının oluşumu gösterilmiştir.

e1 x s49 –> c1 e1 x s49 -> c1

e2 + s50 –> c2 e2 + S50 -> C2

e3 + s51 –> c3 e3 + s51 -> c3

e4 x s52 –> c4 E4 x s52 -> c4

Meydana gelen sonuçlar bir öncekilerle tekrar XOR işlemi uygulanarak yeni 4 tane değer elde edilir. Bu uygulamalar 8 kez tekrarlanır.Son 4 anahtar kullanılarak yeni oluşan 4 değerin birincisi ile 49. anahtar çarpım, ikincisi ile 50. Anahtar toplama, üçüncüsü ile 51. Anahtar toplama ve 52. Anahtar ile çarpım işlemleri yapılarak şifreli metin elde edilir.

Şifrenin çözülmesinde bu algoritma simetrik algoritma yöntemi olduğu için aynı şifreleme algoritması kullanılarak tersi alınmış anahtar seti ile oluşturulmaktadır. Algoritmasını incelersek;

Şifre çözülmesi için yine aynı şifreleme algoritması bu sefer ters i alınmış key seti ile yapılmaktadır. Aşağıdaki tabloda İDEA şifreleme örneği verilmiştir. X1, X2, X3 ve X4 şifrelenmemiş metindir.

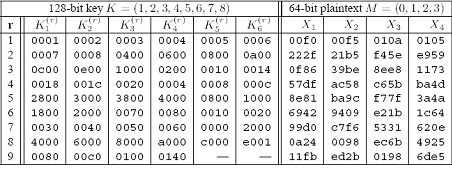
İDEA ya saldırı yöntemi için en etkilisi kaba kuvvet yöntemidir. Bu anahtarı tespit edebilmek için 2128(1038) şifreleme gerektirir.

Şifrenin Çözümlenmesi

Şifrenin çözümlenme işleminden yukarıda kısaca bahsedilmişti. Bunu formül halinde görmek istesek ;

The first four subkeys for decryption are: Şifre çözme için ilk dört alt anahtarlar şunlardır:

KD(1) = 1/K(49) KD (1) = 1 / K (49)

KD(2) = -K(50) KD (2) =-K (50)

KD(3) = -K(51) KD (3) =-K (51)

KD(4) = 1/K(52) KD (4) = 1 / K (52)

Yani şifreleme de uygulanan işlemlerin ters işlemleri uygulanarak aynı algoritma kullanılarak şifre çözümleme işlemi yapılabilmektedir.

Şifrelem işleminde modüler çarpım işlemi yapılmaktaydı. ((2^16)+1) ile (2^16) nın modüler çarpım işlemi şeklinde ifade edilmekteydi. Şifre çözme işlemleri yapılırken bu detayın göz önünde bulundurulması gerekmektedir.

Aşağıdaki şekilde detaylı gösterim yapılmaktadır ;

1st round s49* s50# s51# s52* s47 s48

2nd round s43* s45# s44# s46* s41 s42

3rd round s37* s39# s38# s39* s35 s36

4th round s31* s33# s32# s34* s29 s30

5th round s25* s27# s26# s28* s23 s24

6th round s19* s21# s20# s22* s17 s18

7th round s13* s15# s14# s16* s11 s12

8th round s7* s9# s8# s10* s5 s6

Final transformation…..s1* s2# s3# s4*

sXX* = multiplicative inverse of sXX modulus ((2^16)+1)

sXX# = additive inverse of sXX modulus (2^16)

Aşağıda, şifrenin çözülmesi için bir tabloda örnek verilmiştir.

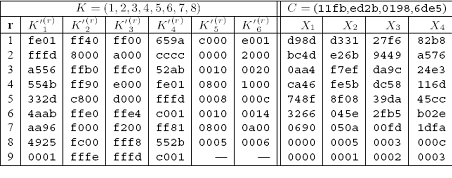
Test

Kodlamada tüm değişkenler tekrar tekrar gözden geçirilmiştir ve şifreleme veya şifre çözme işlemleri esnasında herhangi bir olumsuz durum yaşanmamıştır.

İdea’ nın mevcut yazılım uygulamaları, DES in hemen hemen iki katı kadar hızlı çalışır. IDEA saniyede 33 mhz ile 386 makine üstündeki 880 kbitlik datayı şifreleyebilir ve 2400 kilobit lik datayı 486 makinenede 66 mhz le şifreleyebilmektedir. İdea hızlıymış gibi bir tablo karşımıza çıkabilir ama çarpımları ucuz değildir. İki 32 bitlik sayıyı çarpmak için 40 saat çevriminin üstünde zaman gerekir.

PES’ in VLSI uygulaması, 55 megabitlik veriyi saniyede 25 mhz ile şifreler. 107.8 milimetrekare bir çip, idea algoritmasıyla saniyede 177 megabit veri şifreleyebilmektedir.

Sonuç

İDEA algoritması bir blok şifreleme yöntemidir ve şifreleme ile şife çözme algoritması aynı olduğu için simetrik algoritmalar sınıfındadır. Çeşitli matematiksel işlemler kullanılarak, karmaşık işlemler bu algoritmanın matematiksel zorluğunu ortaya koymaktadır.Yazılan kodla birlikte bu şifreleme yönteminin anlaşılması pekişmiştir.

Referanslar

http://www.finecrypt.net/idea.html,

http://www.olympos.org/belgeler/bxa/kriptografi-bolum-1-simetrik-kriptografi-5549.html

http://www.quadibloc.com/crypto/co040302.htm

http://www2.itu.edu.tr/~orssi/thesis/2008/Vijlan_Celik_bit.pdf

http://www.evrencomert.com/sayfa/assets/Dosyalar/Depo/Cesitli/Kripto_Algoritmalar.html

http://doctus.org/makale-ssh-nedir-t601.html

http://linux.about.com/cs/linux101/g/IDEA__Internati.htm

http://islab.oregonstate.edu/koc/ece575/04Project2/Miller/algorithm.JPG

İlgili Yazılar

PGP (Pretty Good Privacy)

Digital Signature Transponder CipherDST 40 Algoritması

Security Protocol Notation (Güvenlik Teşrifat Yazımı)

Lowe Saldırısı (Lowe Attack)

Giz Paylaşımı (Secret Sharing, Sır Paylaşımı)

İnkar Edilebilir Şifreleme (Deniable Encryption)

Bir cevap yazın Cevabı iptal et