Pohlig Hellman Algoritması

Yazan : Şadi Evren ŞEKER

Steven Pohlig ve Marin Hellman tarafından geliştirilen, ayrık logaritma probleminin (discrete logarithm) çözümü için bir alternatif sunan algoritmadır.

Algoritma basitçe aşağıdaki denklemde bulunan x değerine bir çözüm arar:

e ≡ g^x (mod p)

Bu durum tam olarak da ayrık logaritmanın tanımıdır ve yukarıdaki denklem, aşağıdaki hale dönüştürülebilir:

x ≡ log_g e (mod p)

Algoritma birkaç adımdan oluşur.

1. Ayrık logaritması hesaplanacak olan grubun (g) asal çarpanlarının bulunması. Bu aşama için totient fonksiyonu (totient function) kullanılır.
2. Birinci adımda bulunan değerler için çin kalan teorisinin kullanılması (chineese remainder theorem) ve her çarpan için ayrı bir denklem elde edilmesi. Bu aşamada da daha hızlı sonuca ulaşmak için bebek ve dev adımları algoritmasını (baby step giant step) kullanabiliriz
3. İkinci adımın bütün asal sayılar için tekrarlanması
4. İkinci ve üçüncü adımların tekrarlanması sonucunda elde edilen denklemlerin çin kalan teoremi ile çözümü.

Yukarıda adımları verilen bu algoritmanın çalışmasını bir örnek üzerinden görerek anlamaya çalışalım.

Örneğin ayrık logaritmasını bulmak istediğimiz denklem aşağıdaki şekilde verilmiş olsun.

x ≡ log₆ 7531 (mod 8101)

Daha açık olması açısından, yukarıdaki denklemi, aşağıdaki şekilde de yazabiliriz.

7531 ≡ 6^x (mod 8101)

Öncelikle totient fonksiyonu bulmak için çarpanlarına ayırma işlemi yapıyoruz:

p-1 = 8101 – 1 = 8100 = 2²3⁴5² olarak yazılabilir. (Lütfen Ferma’nın küçük teoremini hatırlayınız (Fermat’s little theorem))

Yukarıda elde edilen bu değerler Çin kalan teoremine göre aşağıdaki şekilde bir denkleme işaret eder:

x₂ ≡ x mod (2²)

x₃ ≡ x mod (3⁴)

x₅ ≡ x mod (5²)

Yukarıdaki denklemleri yerine yazacak olursak:

x₂ ≡ x mod (4)

x₃ ≡ x mod (81)

x₅ ≡ x mod (25)

Yukarıdaki denklemlerin her birini ayrı ayrı çözüp aynı x değeri için beklenen x₂,x₃ ve x₅ değerlerini bulmaya çalışalım.

İlk olarak x₂ değerini hesaplamaya çalışıyoruz. Denklemimizdeki mod işlemi 2² olduğu için 2 tabanında çift değer hesaplanacaktır.

x₂=c₀ (2)⁰+c₁(2)¹ ,olarak yazılabilir.

Bu denklemdeki çarpanları, aşağıdaki şekilde yapabiliriz:

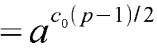
İkinci çarpan için de aşağıdaki denklemi bulacağız:

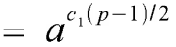
İlk denklemi çözerek başlayalım.

7531 ^(p-1)/2 = 7531 ⁴⁰⁵⁰ = -1, bunun anlamı, c0 değerimizin vâr olduğu ve 1 olduğudur.

İkinci denklemi çözmek için ilk denklemden elde ettiğimiz sonuca, 7531’i bölüyoruz.

7531(a)^-1 = 7531(6751) = 8006 mod 8101

8006 ^(p-1)/4 = 8006 ²⁰²⁵ = 1 ve dolayısıyla c₁ değerini 0 olarak buluyoruz. (yukarıdaki ikinci denklemde sadece a⁰ =1 olacağı için c₁(p-1)/2 değeri olacaktır ve bu durumda 0 veren tek c₁ değeri 0’dır.)

x₂ denklemine dönüp denklemimizi yeniden yazalım:

x₂ = c₀ (2)⁰+ c₁(2)¹ = 1 + 0 (2) = 1

dolayısıyla Çin kalan teoremindeki ilk denklemimiz:

1 ≡ x mod (2²) olarak bulunmuş olunur.

Gelelim ikinci denklemimize,

x₃ ≡ x mod (3⁴)

4ncü dereceden olan denklemin çözümü için aşağıdaki denklemi yazabiliriz:

x₃ = c₀ (3)⁰ + c₁ (3)¹ + c₂ (3)² + c₃(3)³ yazılabilir. Bu denklemi ilerletirsek:

x₃ = c₀ + 3c₁ + 9c₂ + 27c₃ şeklinde yazabiliriz. Denklemimizdeki çarpanları teker teker bulalım:

7531 ^(p-1)/3 mod 8101 = 2217 buradan c₀ = 2 olarak bulunur.

Sıradaki çarpan olan c1’i bulmak için önce 7531 sayısını c0’a bölüyoruz:

7531 / 2 = 6735 mod 8101 bulunuyor. Ve c₁ için denklemi çözüyoruz:

6735 ^(p-1)/9 = 1 dolayısıyla c₁ = 0 olarak bulunuyor.

6735 değerini a^3c1 değerine bölüyoruz 6735 / a₀ = 6735 mod 8101 ve denklemimizi yazıpyoruz:

6735^(p-1)/27 = 2217 olarak bulunuyor ve c₂ = 2 sonucuna varıyoruz. Son olarak c₃ hesaplayabilmek için 6735 / a^9c2 değerini hesaplıyoruz:

6735 / a¹⁸ = 6992 mod 8101 olarak bulunuyor.

Denklemimizi yazarsak

6992 ^{(p-1) / 81} = 5883 olarak bulunuyor ve bu değere göre c₃ = 1 bulunuyor.

Denklemimizi yeniden yazarsak:

x₃ = c₀ + 3c₁ + 9c₂ + 27c₃

x₃ = 2 + 3 0 + 9 2+ 27 1

x₃ = 47 olarak bulunur. Bu durumda çin kalan teoremindeki ikinci denklemimiz aşağıdaki şekildedir:

47 ≡ x mod (3⁴)

Gelelim son denklemimize:

x₅ ≡ x mod (5²)

Denklemimiz ikinci dereceden olduğu için x₅ denklemini aşağıdaki şekilde iki çarpanla yazabiliriz:

x₅ ≡ c₀ + 5c₁

7531^(p-1)/5 = 5221 dolayısıyla c₀ = 4 olarak bulunur.

Bölme işleminden sonra 7531 / a₄ = 7613 mod 8101

7613^(p-1)/25 = 356 dolayısıyla c₁ = 2 olarak bulunur.

Denklemimizi yeniden yazacak olursak

x₅ = 4 + 2 5 = 14 olarak bulunur ve denklemimiz:

14 ≡ x mod (5²) olarak yazılabilir.

Şimdi yukarıda elde ettiğimiz üç denklemi yeniden listeleyelim :

1 ≡ x mod (2²)

47 ≡ x mod (3⁴)

14 ≡ x mod (5²)

Çin kalan teorisine göre her değerin tersini bulup çarpalım:

4 x 81 x 25 = 8100

8100 / 4 = 2025 ve 2025’in mod 4 için tersi 1

8100 / 81 = 100 ve 100’ün mod 81 için tersi 64

8100 / 25 = 324 ve 324’ün mod 25 için tersi 24 olarak bulunur. Denklemde yerine yazarsak:

X = 1 2025 1 + 47 100 67 + 14 324 24 = 6689 mod 8101 olarak bulunmuş olunur.

Şimdi sorunun başına dönüp sağlamamızı yapalım:

7531 ≡ 6^x (mod 8101)

Denkleminde x = 6689 olması durumu için denk oldukları görülebilir.