Bayes Ağları (Bayesian Network)

Yazan : Şadi Evren ŞEKER

Bilgisayar bilimlerinde veri modelleme ve durum geçişi ifade etmek için kullanılan yöntemlerden birisidir. Literatürde bayes network veya blief network (inanç ağı) olarak da geçen ağların özelliğ istatistiksel ağlar olmaları ve düğümler (nodes) arası geçiş yapan kolların (edges) istatistiksel kararlara göre seçilmesidir.

Bayes ağları yönlü dönüşsüz ağlardır (directed acyclic network) ve her düğüm ayrı bir değişkeni ifade eder. Ayrıca bu değişkenler (rastgele değişkenler, random variables) arasındaki sıralama da bayes ağları ile gösterilebilir (basitçe bir düğümden diğer düğüme geçiş sırası).

Bayes ağlarının daha geniş hali de belirsiz karar ağaçlarıdır ( uncertain decision trees).

Bayes ağlarını anlayabilmek için Bayes teoremini hatırlamakta yarar vardır.
Bayes Teoremi :

bu
eşitlik bayes theorem’idir.

Örnek Yay üreten 3 Makine için aşağıdaki hata ve üretim oranları veriliyor:

	Bozuk Yay oranı	İmalattaki oranı
I. Makine	%2	%35
II. Makine	%1	%25
III. Makine	%3	%40

Üretilen yaylardan rasgele birisi
seçildiğinde bozuk olma olasılığı:
P(B)=P(I)P(B|I)+P(II)P(B|II)+P(III)P(B|III),

olarak
hesaplanır.

Eğer yay bozuk çıktıysa bunun 3.
makineden çıkma olasılığı aşağıdaki şekilde hesaplanır:

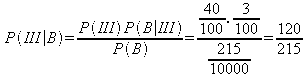
Örnek:

Bütün nufusta yapılan bir
hastalık testinde (+) pozitif sonucun doğru bilinme olasılığı 0.99 ve
(-) negatif sonucun doğru bilinme olasılığı 0.95 olarak veriliyor.
Hastalığın bütün nufusta görülme olasılığı ise
0.0001 ise test sonucu pozitif çıkan bir kişinin hasta olma
olasılığı nedir?

D olayı kişinin hasta olma olasılığı
olsun

D’ olayı kişinin hasta olmama
olasılığını göstermiş olur.

Buna göre P(D) = 0.0001 olur

S olayı ise testin (+) çıkma
olasılığı olsun.

S’ olayı testin (-) çıkma
olasılığını göstermiş olur.

Buna göre P(S’|D’) = 0.95 olduğuna
göre P(S|D’) = 0.05 olur.

Soruda istenen durum P(D|S) ile
gösterilebilir ve şartlı ihtimal hesabından

ancak
burada
Dolayısıyla
bayes teoremini uygulamayı deneyebiliriz. Buna göre

olarak
bulunur. S olayı için iki ihtimal bulunduğundan ( test sonucu
ya (+) ya da (-) çıkabilir) olasılık modeli aşağıdaki şekilde
olur:

olur.
Sonuç ise

olarak bulunur.

« Tuz ve Biber Gürültüsü (Salt and Pepper Noise) | Sezgisel Algoritmalar (Buluşsal Algoritmalar, Heuristic Algorithms) »

Yorumlar

Bu Yazı Hakkında

Bilgisayar Kavramları üzerinde şu anda okumakta olduğunuz 'Bayes Ağları (Bayesian Network)' isimli yazı 21 Dec 2008 tarihinde, saat: 22:01 'de Şadi Evren ŞEKER tarafından gönderilmiş, toplam 1227 defa okunmuştur.

Benzer yazıları Bilgisayar Kavramları, Yapay Sinir Ağları (Artificial Neural Networks), bilgisayar felsefesi, veri yapıları, yapay zeka (artificial intelligence) kategorilerinden okuyabilirsiniz. Yazar ile irtibat kurmak için email gönderebilirsiniz. Yazıya yorum yapabilir ya da yapılan yorumları RSS 2.0 ile takibe alabilirsiniz.

Yazarın Kitabı

Bu yazının yazarı Şadi Evren ŞEKER'in son çıkan kitabı "Programlama ve Veri Yapılarına giriş (C, C++ ve JAVA ile)" hakkında bilgi almak için Buraya tıklayabilirsiniz.
Eklenen Son Yazılar