İki Parçalı Graflar (Bipartite Graphs)
Yazan : Şadi Evren ŞEKER
İçerik
1. İki parçalı graflara örnekler
2. İki parçalı grafın test edilmesi
3. İki parçalı grafların kullanım alanları
4. İki parçalı grafların özellikleri
Bilgisayar bilimlerinde veri modellemede sıkça kullanılan grafların (graph) özel bir durumudur. Buna göre bir graf’ı oluşturan düğümleri iki farklı kümeye ayırabiliyorsak ve bu iki kümenin elemanlarından küme içerisindeki bir elemana gidilmiyorsa. Yani bütün kenarlar (edges) kümeler arasındaki elemanlar arasındaysa, bu graflara iki parçalı graf (bipartite graph) ismi verilir.
Örneğin aşağıdaki şekilde gösterilen graf’ın iki parçalı olup olamayacağını incelemeye çalışalım:

Yukarıda örnek olarak verilen garfın düğümlerini koşulumuzu sağlayacak şekilde yani iki ayrı küme oluşturacak ve bu kümelerin içerisinde yol bulunmayacak şekilde yerleştirmeye çalışalım.
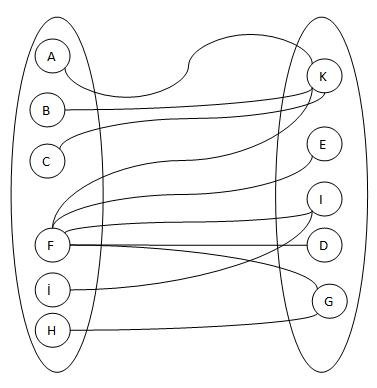
Yukarıdaki şekilde, ilk şekilden farklı olarak sadece düğümlerin (nodes) yerleri değiştirilmiştir. Yukarıdaki şekilde ayrıca iki ayrı küme oluşturulmuş ve ilk küme ile ikinci küme arasında bölünen düğümlerin tamamında kenarlar karşı kümeye işaret etmiştir. Yani aynı küme içerisinde hiçbir kenar bulunmamaktadır.
Bu durumu aşağıdaki şekilde de gösterebilirdik:
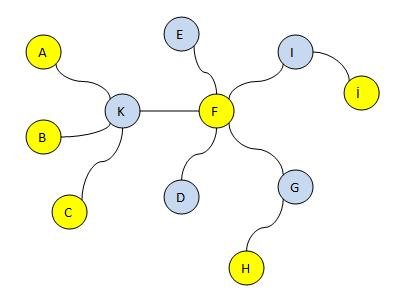
Yukarıdaki şekilde görüldüğü üzere komşu olmayan düğümler renklendirilmiştir. Yani komşu iki düğüm aynı renkle renklendirilmemiştir. Daha farklı bir deyimle bir düğümün komşuluk listesindeki (adjacency list) bütün düğümler aynı renkte boyanmıştır. Sonuçta aynı renkte boyanan iki komşu oluşmamaktadır.
Aşağıdaki iki parçalı olmayan grafta aynı şekilde yaklaşırsak problem orataya çıkacaktır.
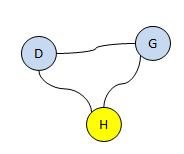
Yukarıdaki şeki bipartite tree (iki parçalı ağaç) değildir. Çünkü graftaki D ve G aynı renktedir. Bu düğümlerden birisinin rengi değiştirildiğinde bu sefer de H ile aynı renkte olacaktır. Dolayısıyla hiçbir şekilde iki grup elde edilemez. Farklı bir ifadeyle:
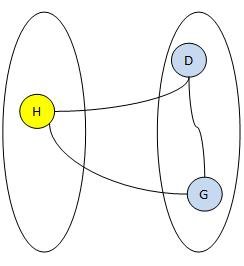
Grafı yukarıdaki şekilde iki gruba bölmek istersek görüldüğü üzere aynı gruptaki iki düğüm arasında bir kenar bulunmakta bu durumda da iki parçalı ağaç olamamaktadır.
İki parçalı grafın test edilmesi
Bir grafın iki parçalı olup olmadığını (bipartite) test etmek için ne yazık ki yukarıda gösterildiği gibi graftaki bütün düğümlerin yerlerinin değiştirilmesi iki kümede toplanması ve sonunda da aralarında bir kenar olup olmadığına bakılması mümkün değildir.
Bir grafın iki parçalı olduğunu anlamak için grafın bütün elemanları arasında tek ve çift ayrımı yapılabilir. Örneğin rast gele seçilen bir düğümden başlanarak diğer bütün düğümlerin bu düğüme olan mesafesini yazmamız ve neticesinde tek ve çift düğümlerin komşuluğunu kontrol etmemiz yeterlidir. Yani çift veya tek iki düğüm birbirine komşu değilse bu grafa iki parçalı graf ismi verilebilir.
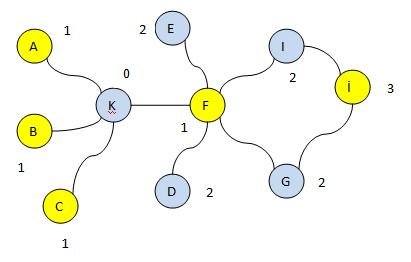
Yukarıdaki şekilde başlangıç için rast gele olarak 0 seçilmiş olsun. Bu grafta K düğümüne olan uzaklıklarına göre bütün düğümlere mesafeleri yazılmıştır. Örneğin İ düğümü K düğümüne 3 düğüm uzaklıktadır. Sonrada bütün düğümler tek ve çift olmasına göre renklendirilmiştir. Yani tek sayıdaki uzaklıkta olanlar sarı, çift sayıdaki uzaklıkta olanları ise mavi boyanmıştır. Bu boyama sadece görüntüleme için kullanılmıştır.
Programlama sırasında bilgisayar tek ve çift sayıdaki düğümleri kontrol edebilir. Örneğin G ve İ düğümleri komşudur. Benzer şekilde İ ve I düğümleri de komşudur. Şayet bu düğümler bir şekilde aynı şekilde olsaydı (ikiside çift veya ikisi de tek olsaydı) bu durumda iki parçalı bir grafik değildir sonucuna varılacaktı.
İki parçalı grafların kullanım alanları
Özellikle eşleştirme problemleri için oldukça kullanışlıdırlar. Eşleştirme problemleri (matching problems) genelde iş/işçi eşleştirmesi, evlilik, problem / çözüm eşleştirmesi gibi farklı unsurları birleştirmek için kullanılırlar.
Örneğin k kişisi i işi için uygunsa k kişisi ile i işi arasında bir kenar bulunuyor demektir. Bu iş ve kişilerden oluşan grafikte atama hatalarının olup olmadığının bulunması iki parçalı ağaç bulan algoritmalar için oldukça basittir.
Örneğin paralel işleme (eş zamanlı işleme) ve koşut zamanlı işleme (concurrent processing) gibi aynı anda birden fazla işin beraber yapıldığı işlerde kullanılan petri ağları (Petri nets, place / transition nets) gibi ağların modellenmesinde ve çalıştırılmasında önemli rol oynarlar.
iki parçalı grafların özellikleri
iki parçalı graflar için aşağıdaki çıkarımlar ve koşullar sıralanabilir:
- Bütün ağaçlar iki parçalı graftır.
- Şayet bir graf döngü (cycle) içermiyorsa iki parçalı graftır.
- Şayet bir graf tek sayıda düğümden oluşan bir döngü (cycle) içeriyorsa iki parçalı graf değildir.
- Şayet bir graf boyandığında iki renk veya daha az renkle boyana biliyorsa bu graf iki parçalı graftır. (detaylı bilgi için graf boyama (graph coloring) başlıklı yazıyı okuyabilirsiniz)


