Öyler Yolu (Eulerian Path)
Yazan : Şadi Evren ŞEKER
Bilgisayar mühendisliği de dahil olmak üzere pekçok bilim ve mühendislik alanında kullanılan graf teorisindeki özel bir yol (path) şeklidir. Bu yolun özelliği her kenardan (edge) bir kere (en az ve en çok) geçen yolu bulmaktır.
İçerik
Teorinin tarihi çıkışı
Teorinin tanımı
Öyler yollarının özellikleri
Bir graftaki farklı öyler yollarının sayısı
İlk bakışta hamilton yolu (hamiltonian path) ile karıştırılabilir ancak Hamilton yolundaki amaç her düğümden (node) bir kere geçen yolu bulmak iken Öyler yolunda her kenardan (edge) bir kere geçen yolu bulmak amaçlanır.
Öyler teorisinin tarihi çıkışı
Öylerin teorisini ortaya atmasında önemli rol oynayan tarihi problem Königsberg köprüsü problemidir.

Yukarıdaki şekilde pregel nehri etrafında kurulu (C ve B karaları) ve nehrin ortasında iki adası olan (A ve D adacıkları) kösigner şehrinin yukarıda görülen 7 köprüsü bulunmaktadır.
Problem bütün köprülerden bir kere geçilen bir yol olup olmayacağıdır.
Öyler bu soruyla uğraşırken yazımızın konusu olan öyler yolu teorisini bulmuştur ve cevap olarak böyle bir yolun bulunamayacağını istaplamıştır.
Öylerin iddiası bastir bir keşfe dayanmaktaydı. Şayet bir düğüme (node) bir kenar (edge) ile geliniyorsa bu düğümü terk etmek için farklı bir yola ihtiyaç duyulur.
Bu durumda her düğümün sini (node order) hesaplayan Öyler, bir düğüme giren çıkan yolların sayısına düğüm si (node order) ismini verdi.
Buna göre şayet bir düğümün si tekse, bu düğüm ya başlangıç ya da bitiş düğümü olmalıdır. Bunun dışındaki durumlarda (yol (path) üzerindeki herhangi bir düğüm olması durumunda) tek sayıdaki yolun sonuncusu ziyaret edilmiş olamaz.

Yukarıdaki şekilde köprü örneğinin graf ile gösterilmiş hali görülüyor. Burada dikkat edilirse her dört düğüm de tek sayıda ye sahiptir.
A 5
B C D ise 3
sine sahiptir. Bu durumda düğümlerden iki tanesi başlangıç ve bitiş olsa diğer iki tanesini birleştiren yollar kullanılamayacak ve bütün kenarlar gezilmiş olamayacaktır.
Öyler yolu (eulerian path) tam olarak şu şekilde tanımlanabilir:
Bir yönsüz grafta (undirected graph) şayet bütün düğümleri (nodes) dolaşan bir yol bulunabiliyorsa bu yola Öyler yolu( Eulerian Path, Eulerian Trail, Eulerian Walk) ismi verilir. Bu yolun bulunduğu grafa ise yarı öyler (semi-eulerian) veya dolaşılabilir (traversable) graf ismi verilir.
Şayet bu yolun başlangıç ve bitiş düğümleri (node) aynıysa bu durumda tam bir döngü (cycle) elde edilebiliyor demektir ve bulunan bu yola öyler döngüsü (eulerian cycle, eulerian circuit veya eulerian tour) ismi verilir. Bu yolu içeren grafa ise öyler grafı (eulerian graph veya unicursal) ismi verilir.
Yukarıdaki tanımı yönlü graflar (directed graphs) için de yapmak mümkündür. Ancak bu durumda yukarıdaki tanımda geçen yolları, yönlü yollar ve döngüleri, yönlü döngüler olarak değiştirmek gerekir.
- Bir yönsüz bağlı grafın bütün düğümlerinin si çiftse bu graf öyler grafıdır (eulerian) [amcak ve ancak]
- Bir yönlü graf (directed graf) ancak ve ancak bütün düğümlerin giren ve çıkan lerinin toplamları eşitse öyler grafı (eulerian) olabilir.
- Bir yönsüz graf’ın öyler yolu bulunabilmesi için iki veya sıfır sayıda tek düğüm sine sahip üyesi olmalıdır.
Bir grafta öyler döngüleri bulunuyorsa, birden fazla olabilir. Yani birbirinden farklı döngüler elde edilebilir. Burada fark oluşturan faktör başlangıç ve bitiş düğümleridir.
Örneğin aşağıdaki şekil için
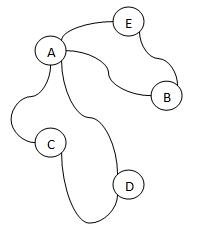
A-B-E-A-C-D-A döngüsü bir öyler döngüsüdür. Benzer şekilde
E-B-A-C-D-A-E döngüsü de bir öyler döngüsüdür.
Buradaki soru acaba bir grafta kaç farklı öyler döngüsü olabilir?
Bu soruya cevap BEST teoremi ismi verilen ve teoremi bulan kişilerin isimlerinin baş harflerinden oluşsan teorem ile verilir. BEST teoremine göre bir grafta bulunan öyler döngülerinin sayısı graftaki bütün düğümlerin lerinin bire eksiğinin faktöriyellerinin çarpımına eşittir.
∏ ( d(v)-1) !
olarak gösterilebilecek teoriye göre d() verilen düğümün (vertex) si ve v ise graftaki bütün düğümlerdir.
Örneğin yukarıdaki graf için bu değeri hesaplayacak olursak önce düğümlerin lerini çıkarmamız gerekir:
A 4
B 2
C 2
D 2
E 2
Şimdi bu değerlerin birer eksiklerinin faktöriyellerini çarpalım
3! = 6
1! = 1
1! = 1
1! = 1
1! = 1
sonuç olarak 6x1x1x1x1 = 6 farklı öyler döngüsü bulunabilir diyebiliriz.



bu gerçekten başarılı bir site gerçekten bravo!
Çok teşekkürler güzel anlatım
Merhaba hocam. Ben sıkı bir takipçinizim. Evet ‘takipçi’; pop yıldızlarını ya da sporcuları takip etmekten farklı bir durum bir bilişimciyi sıkı takip etmek. Gerçekten çok iyisiniz. Hem bilgi hemde insanlık açısından. Trabzon’da okuyorum buraya geldiğinizde de sizi dinlemek için geldim dinledim. Big Data’yı anlatmıştınız. Bilgilerinizi sürekli insanlarla paylaşmak, insanlara bu denli yardımcı olmaya çalışmak ve akabinde de yardımcı olmak gerçekten takdire şayan bir şey. Emeğinize sağlık. İyi ki varsınız.