Yerleşim Sıralaması (Topological Sort, İlinge Sıralaması)
Yazan: Şadi Evren ŞEKER
Bilgisayar bilimlerinde, yönlü dairesel olmayan şekiller (directed acyclic graphs) üzerinde çalışan bir sıralama algoritmasıdır (sorting algorithm). Algoritma tanımı itibariyle tek köklü ve çok köklü ağaçlar (tree) üzerinde çalışmak için tasarlanmıştır denilebilir. Örneğin aşağıdaki ağacı ve sıralama algoritmasının çalışması sonucunda elde edilen neticeyi inceleyerek konuyu anlamaya başlayalım:

Yukarıdaki şeklin, yerleşim sıralaması aşağıdakilerin herhangi birisi olabilir:
5783219
5782319
5781291
5873219
5872319
5871291
5732819
5723819
5732891
5723891
5819732
5891732
5819723
5891723
Görüldüğü üzere yerleşim sıralamasındaki amaç, bir şekilde daha üst seviyede bulunan, veya bir düğümü göstermekte olan diğer düğümün, sıralama sonucunda daha önce gelmesidir. Yukarıdaki şekilde örneğin 5 numaralı düğüm, 7 ve 8 numaralı düğümleri işaret etmektedir. Bu durumda, sıralama sonucunda hiçbir şekilde 7 veya 8, 5’ten önce gelemez.
Yukarıdaki örnek, tek köklü bir ağaçtır ve bu ağaçta sıralama sonucunda her zaman için kök düğüm (yukarıdaki örnekte 5 numaralı düğüm) sıralama sonucunun başında yer almalıdır. Ancak yerleşim sıralaması algoritması (toplogy sort algorithm) birden fazla kökü bulunan şekiller için de çalışmaktadır. Bu durumda, kök olan bütün düğümler aynı seviyede kabul edilir. Örneğin aşağıdaki şekli ele alalım:

Yukarıda verilen yerleşimin sıralanma alternatifleri aşağıda listelenmiştir:
437219
473219
347219
374219
734219
743219
437129
473129
347129
374129
734129
743129
…
Yukarıdaki sonuçların elde edilmesini sağlayan algoritmayı aşağıdaki şekilde tanımlayabiliriz:
A: Boş bir liste olsun (veya dizi)
Şekil üzerinde (graph) kendisine gidilmeyen bir düğüm varken
Bu düğümü alıp A listesine ekle
düğümü şekilden (graph) sil
Görüldüğü üzere sıralama algoritmasında kendisine gidilmeyen düğümlerden herhangi birisini (ki bu düğüm aslında köklerden birisidir) alarak ilerliyoruz. Bu düğüm silindikten sonra yeni kökler çıkıyor. Örneğin yukarıdaki şekil sıralanırken aşağıdaki adımlardan geçebilir:

Sırlama için örneğin 4’ü alalım. Sonuç : 4

Bu düğüm silindi artık yeni köklerimiz : 2,3,7 oldu ve biz örneğin 2’yi alalım. Sonuç : 42
Yeni halinde alabileceğimiz kök düğümler sadece 3 ve 7’dir. Örnek olarak 7’yi alalım. Sonuç 427

Yeni halinde sadece 3 alınabilir çünkü diğer düğümlerin hepsine (1 ve 9) bir şekilde gidilen bir başka düğüm bulunmaktadır. Sonuç 4273

Son olarak sırasıyla 1 ve sonrada 9’u alırsak sıralama işlemimiz tamamlanmış olur: Sonuç 427319 olarak bulunur.
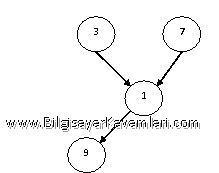
Yukarıdaki algoritmanın, daire içeren bir şekilde (graph) çalışmayacağı barizdir. Bunun sebebi daireye ulaşıldığında bir şekilde kendisine gitmeyen bir düğüm elde edilememesidir. Örneğin graf (graph) aşağıdaki şekilde verilmiş olsun:

Yukarıdaki durumda, ne 9 ne de 1 alınamaz çünkü ikisini de gösteren birer düğüm bulunmaktadır. Bu durumda algoritmamız çalışmaz, zaten yerleşim sıralamasına göre (topological sort) hangi düğümün önce geleceği de belirsizdir.



ellerinize sağlık… çok faydalandım ve teşekkür etmek istedim 🙂
çok güzel hazırlamışsınız elinize sağlık.
5781291 => 5783291 olmali. ufak bir yanlislik olmus.
Teşekkür ederim hocam algroritmanın işleyişini çok iyi anlatmışsınız.
çok teşekkürler,elinize sağlık.
gerçekten çok teşekkürler, çok faydalı oldu.
Guzel, anadolu universitesinde bize yapay zeka dersinde onun yerine PHP verdiler. sizin gibi hocalara ihtiyacimiz var.
Hocam benim kafama takılan yerleşim sıralamasında graflar parçalanabilir mi ?
Bahsettiğiniz, parçala fethet algoritması (aşağıda bağlantısını veriyorum) ile çözülmesi ise, evet çeşitli şekillerde parçalanabilir. Örneğin ağacın tersten gidilmesi mümkündür. Örnek olarak yukarıdaki örnekte 3 adet kökü olan ikinci şekili ele alalım, 9 her durumda sonuncu düğüm olacaktır. Yani demek ki 9’un sonuncu olduğunu kabul ederek bu düğümü silip şekli iki parçaya ayırmanız, ayrılan bu iki farklı şekli iki farklı bilgisayarda sıralayıp sonuca 9’u eklemeniz mümkündür.
http://bilgisayarkavramlari.sadievrenseker.com/2007/12/03/parcala-fethet-yontemi-divide-and-conquer/
Anladım hocam cok teşekkür ederım …
Hocam en uzun yol (longest path) algoritmasının bu işlem ile alakası var mı?