Bu konunun görsel anlatımı eklenmiştir:

Yazan: Şadi Evren ŞEKER

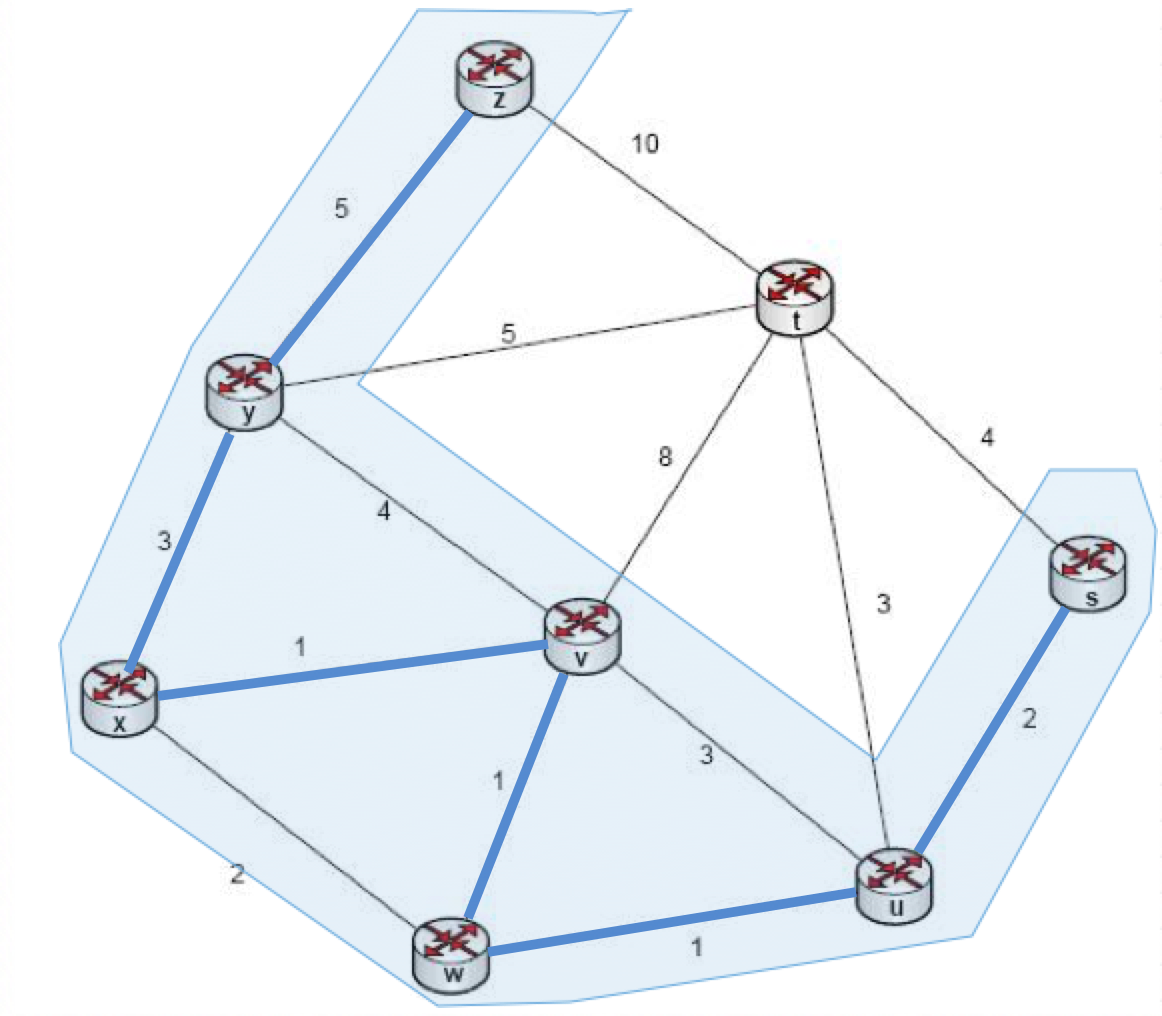
Bir asgari tarama ağacı (minimum spanning tree) algoritması olan Prim algoritması, işaretlemiş olduğu komşuluklara en yakın düğümü bünyesine katarak ilerler. Buna göre aşağıdaki grafiğin asgari tarama ağacını çıkaralım:

Yukarıdaki grafikte her düğüm için bir temsili harf ve her bağlantı için bir ağırlık değeri atanmıştır. Buna göre her düğümden diğerine gitmenin maliyeti belirlenmiştir.

Prim algoritmasında rasgele bir başlangıç noktası seçilir. Örneğin bizim başlangıç noktamız “z” düğümü olsun. Bu durumda ilk inceleyeceğimiz komşuluk, “z” düğümünden gidilebilen düğümler ve maliyetleri olacaktır.

z düğümünden gidilebilen düğümler ve maliyetleri aşağıda listelenmiştir:

y:5
t:10

Prim algoritması bu listedeki en küçük maliyetli komşuyu bünyesine dahil eder. Buna göre yeni üyelerimiz {z,y} olacaktır ve gidilen yollar {z-y:5} olacaktır. (ilk üyeler listesinde şimdiye kadar ziyaret edilmiş düğümler bulunur. Bu düğümler listesinde zaten olan bir düğüm listeye eklenemez. yollar listesinde ise hangi düğümden hangi düğüme ne kadar maliyetle gidildiği tutulur.) Dolayısıyla grafiğimizde Prim algoritması tarafından işaretlenen düğümler aşağıda gösterilmiştir:

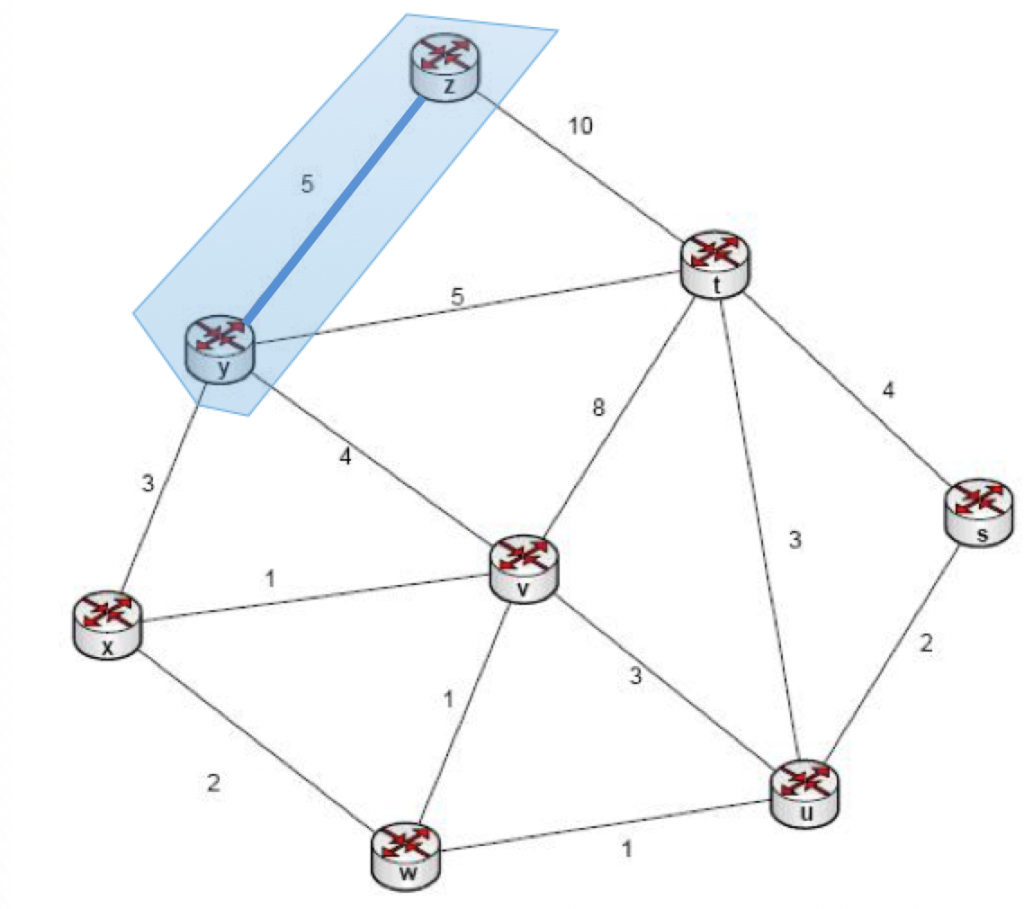
şimdi üyelerimizin durduğu listedeki bütün düğümlerin komşularını listeleyelim:
t:5
t:10
v:4
x:3

yukarıdaki listede t düğümüne iki farklı gidiş bulunmaktadır ( hem z hem de y üzerinden). Biz algoritmamıza devam edip en küçük yolu bünyemize dahil edelim. En yakın komşu x:3′tür. Bu durumda üyelerimiz {z,y,x} olacak ve yollarımız {z-y:5,y-x:3} olacaktır. Bu durum aşağıdaki grafikte gösterilmiştir:

Yeniden komşularımızı listelersek:
t:5
v:1
w:2

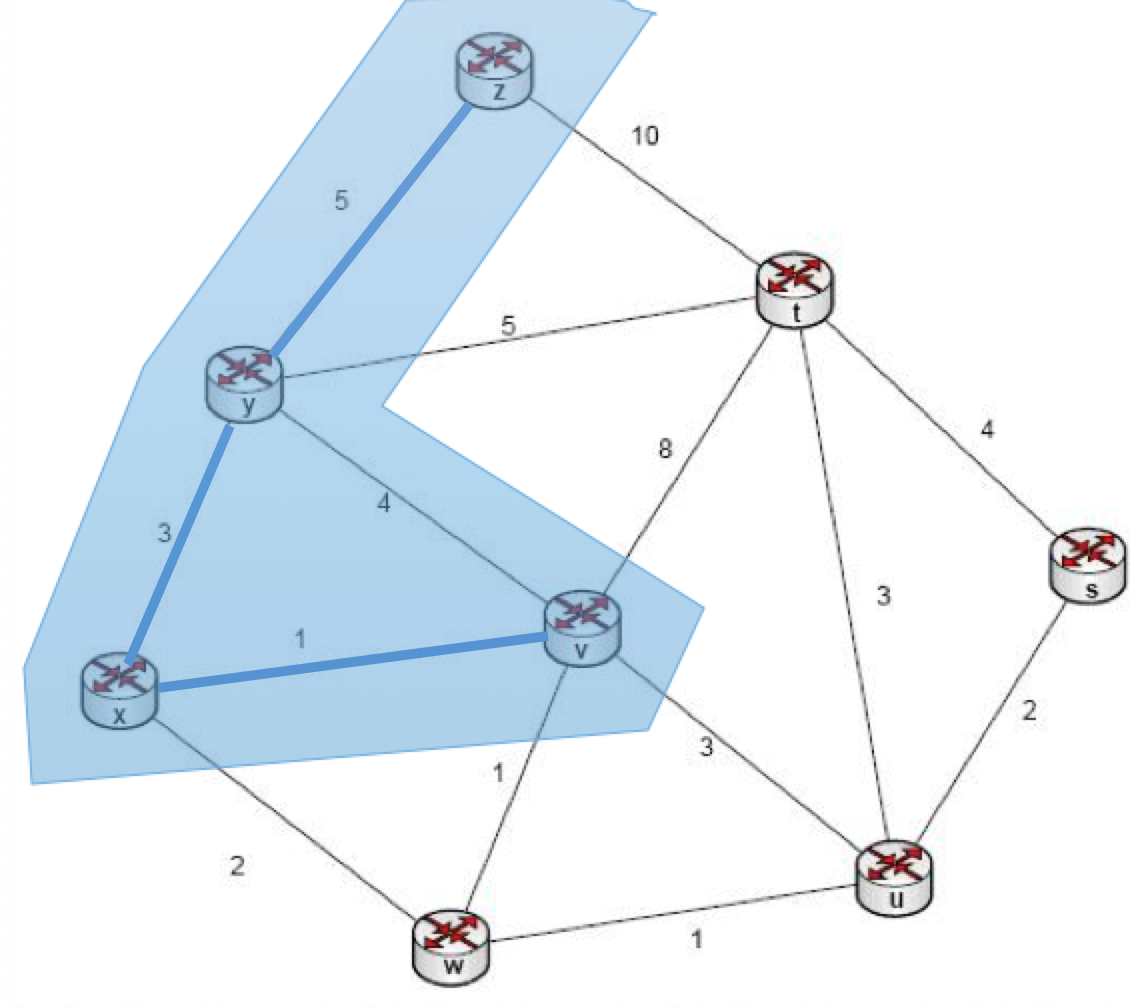
yukarıdaki listede bünyemize aldığımız adadan, bir düğüme giden birden fazla yol bulunması durumunda en kısası alınmıştır. Bu durumda listenin en küçük elemanı olan v:1 tercih edilir ve üyelerimiz {z,y,x,v} yollarımız ise {z-y:5,y-x:3,x-v:1} olur. Durum aşağıdaki grafikte gösterilmiştir:

Yeniden komşularımızı listelersek:
t:5
u:3
w:1

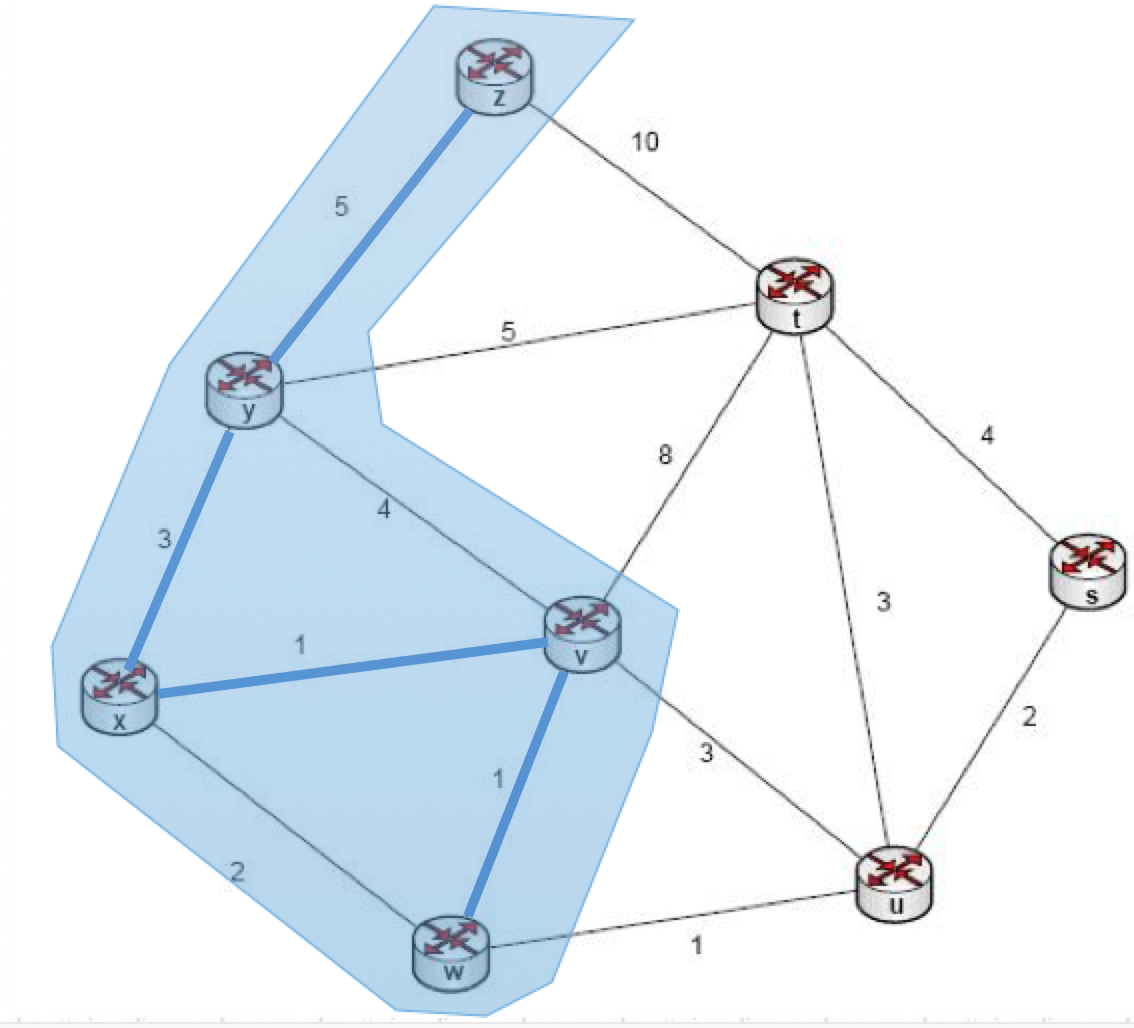
yukarıdaki listede bünyemize aldığımız adadan, bir düğüme giden birden fazla yol bulunması durumunda en kısası alınmıştır. Bu durumda listenin en küçük elemanı olan w:1 tercih edilir ve üyelerimiz {z,y,x,v,w} yollarımız ise {z-y:5,y-x:3,x-v:1,v-w:1} olur. Durum aşağıdaki grafikte gösterilmiştir:

Yeniden komşularımızı listelersek:
t:5
u:1

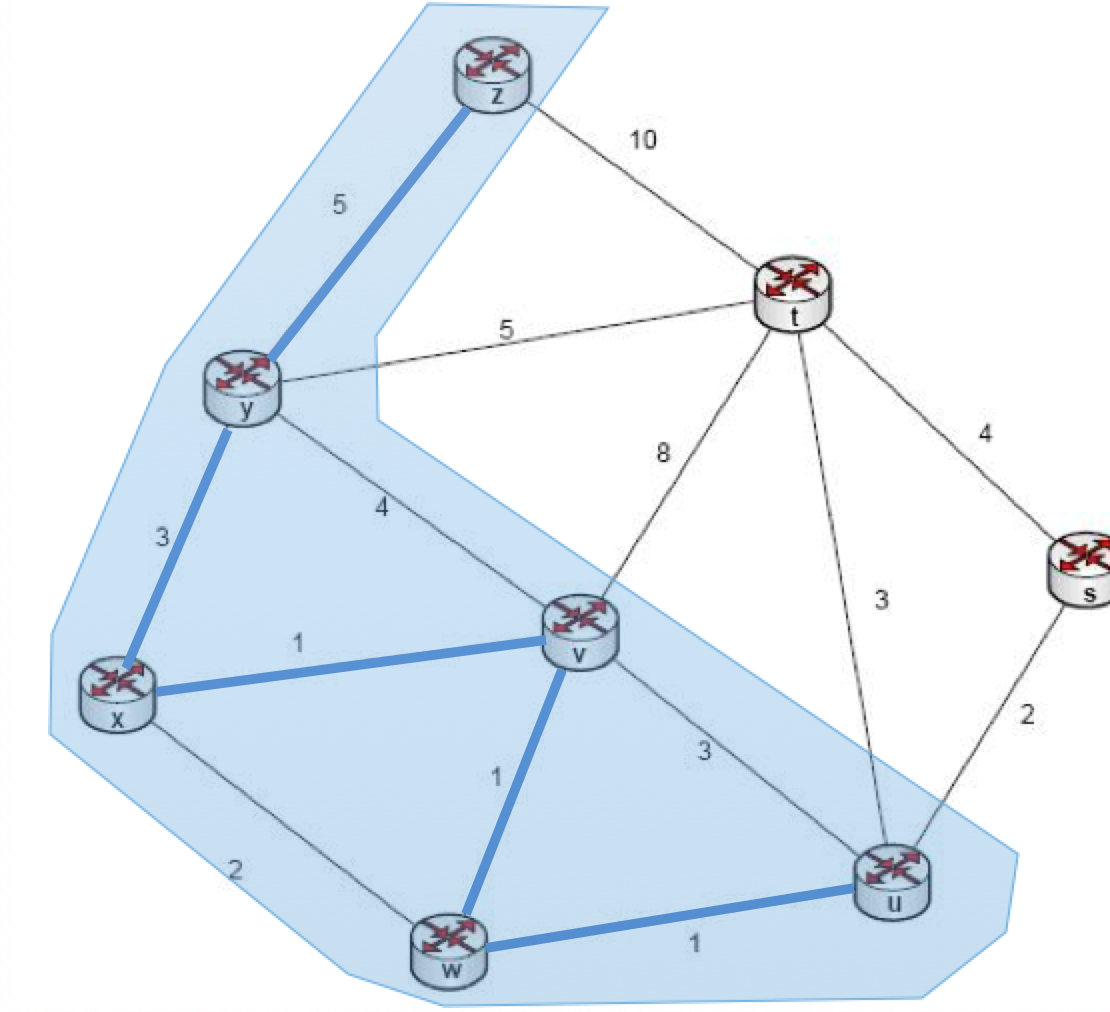
yukarıdaki listede bünyemize aldığımız adadan, bir düğüme giden birden fazla yol bulunması durumunda en kısası alınmıştır. Bu durumda listenin en küçük elemanı olan u:1 tercih edilir ve üyelerimiz {z,y,x,v,w,u} yollarımız ise {z-y:5,y-x:3,x-v:1,v-w:1,w-u:1} olur. Durum aşağıdaki grafikte gösterilmiştir:

Yeniden komşularımızı listelersek:
t:3
s:2

yukarıdaki listede bünyemize aldığımız adadan, bir düğüme giden birden fazla yol bulunması durumunda en kısası alınmıştır. Bu durumda listenin en küçük elemanı olan s:2 tercih edilir ve üyelerimiz {z,y,x,v,w,u,s} yollarımız ise {z-y:5,y-x:3,x-v:1,v-w:1,w-u:1,u-s:2} olur. Durum aşağıdaki grafikte gösterilmiştir:

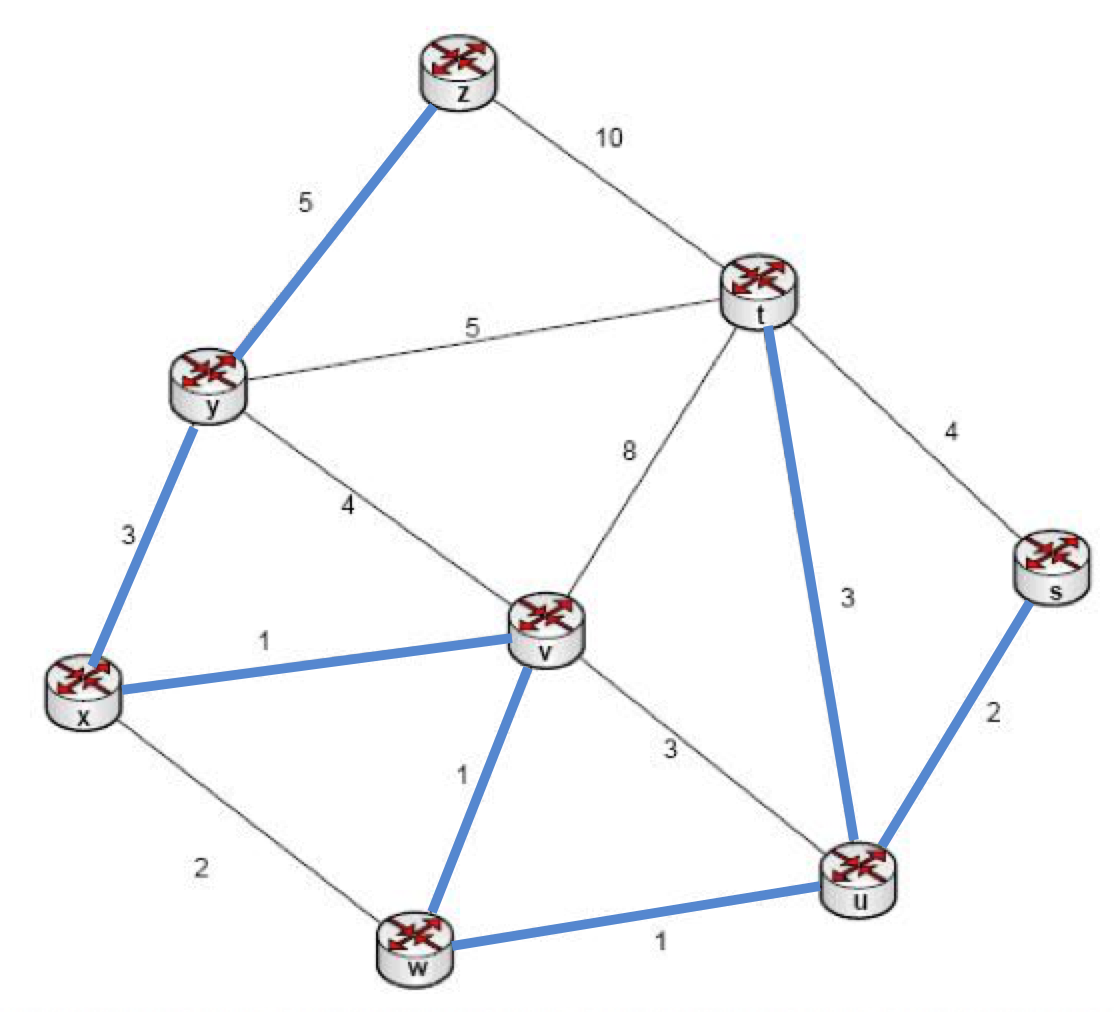
Son komşumuz olan t için en kısa ulaşım
t:3 değeridir ve u üzerinden sağlanır. Bu durumda listenin en küçük elemanı olan t:3 tercih edilir ve üyelerimiz {z,y,x,v,w,u,s,t} yollarımız ise {z-y:5,y-x:3,x-v:1,v-w:1,w-u:1,u-s:2,u-t:3} olur. Sonuçta elde edilen asgari tarama ağacı aşağıda verilmiştir:

1,501 views