Kruskal Asgari Tarama Ağacı Algoritması

Yazan : Şadi Evren ŞEKER

Bir asgari tarama ağacı (minimum spanning tree) algoritması olan Dijkstra algoritması, işaretlemiş olduğu komşuluklara en yakın düğümü bünyesine katarak ilerler. Buna göre aşağıdaki grafiğin asgari tarama ağacını çıkaralım:

Yukarıdaki grafikte her düğüm için bir temsili harf ve her bağlantı için bir ağırlık değeri atanmıştır. Buna göre her düğümden diğerine gitmenin maliyeti belirlenmiştir.

Kruskal algoritmasında bütün yollar listelenip küçükten büyüğe doğru sıralanır. Bu liste yukarıdaki grafik için aşağıda verilmiştir:

x-v:1
w-v:1
w-u:1
x-w:2
u-s:2
x-y:3
t-u:3
u-v:3
y-v:4
s-t:4
y-z:5
y-t:5
z-t:10

Yukarıdaki liste çıkarıldıktan sonra sırasıyla en küçükten en büyüğe doğru komşuluklar işaretlenir. Bu işaretleme sırasında ada grupları ve grupların birbiri ile ilişkisine dikkat edilir. Yani şayet listedeki iki düğüm harfi de aynı adadan ise bu bağlantı atlanır. Aşağıda sırasıyla bu grafikteki adaların oluşması ve asgari tarama ağacının çıkarılması gösterilmiştir:
x-v:1

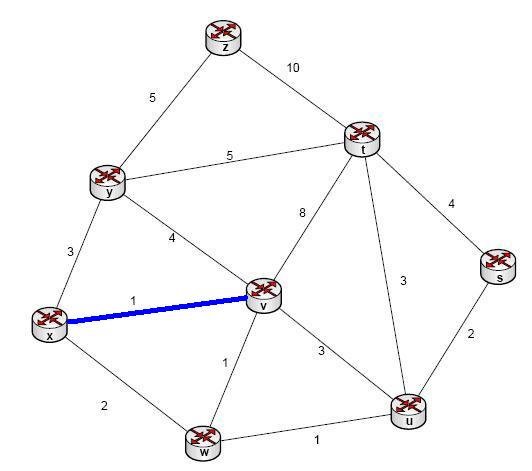
w-v:1

w-u:1

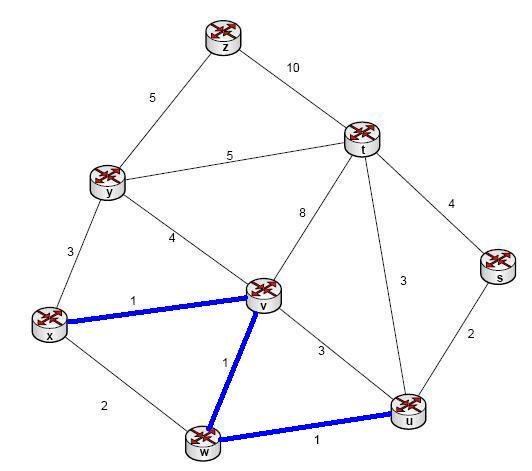
x-w bağlantısı atlanır, çünkü iki düğüm de zaten dolaşılmıştır bunun yerine u-s:2 bağlantısına atlanır.

x-y:3

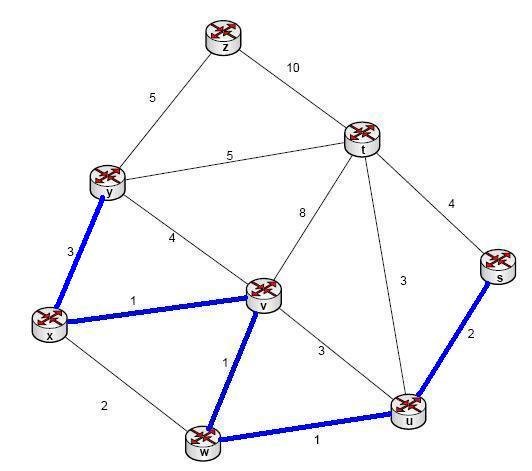
t-u:3

Bu noktadan sonra u-v:3 , y-v:4 , s-t:4 , y-z:5 bağlantılarındaki her iki düğümde aynı adada olduğu için atlanır ve y-t:5 bağlantısına geçilir.

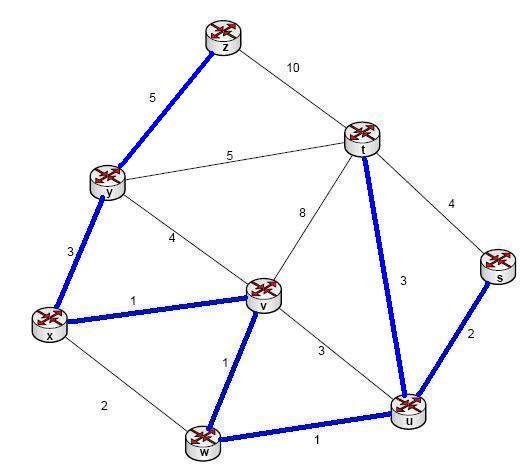
z-t:10 bağlantısı ise iki düğüm de gezildiği için yine gereksizdir.

« Prim asgari tarama ağacı Algoritması | Sonlu Durum Makinası (Finite State Machine, Finite State Automaton) »

Yorumlar

Toplam 2 yorum var.

asgari tarama ağacı (en kısa örten ağaç, minimum spanning tree) : bilgisayar.kavramlari.com | 25 Dec 2007, 13:34
[...] tarama ağacını veren en meşhur algoritmalar: Kruskal Algoritması Prims Algoritması Dijkstra [...]
Hasan Karabasan | 06 Apr 2009, 00:01
Çok teşekkürler…

Bu Yazı Hakkında

Bilgisayar Kavramları üzerinde şu anda okumakta olduğunuz 'Kruskal Asgari Tarama Ağacı Algoritması' isimli yazı 24 Dec 2007 tarihinde, saat: 22:58 'de Şadi Evren ŞEKER tarafından gönderilmiş, toplam 1721 defa okunmuştur.

Benzer yazıları Automata (otomatlar, özdevinirler), Bilgisayar Kavramları, Network(Ağ), Temel Bilimler, algoritma analizi (teory of algorithms) kategorilerinden okuyabilirsiniz. Yazar ile irtibat kurmak için email gönderebilirsiniz. Yazıya yorum yapabilir ya da yapılan yorumları RSS 2.0 ile takibe alabilirsiniz.

Yazarın Kitabı

Bu yazının yazarı Şadi Evren ŞEKER'in son çıkan kitabı "Programlama ve Veri Yapılarına giriş (C, C++ ve JAVA ile)" hakkında bilgi almak için Buraya tıklayabilirsiniz.
Eklenen Son Yazılar