Karatsuba Çarpım Algoritması

Yazan : Şadi Evren ŞEKER

İki tam sayının çarpımı için kullanılan algoritmalardan birisidir. Algoritma temel olarak çok haneli sayıların çarpımında hız kazandırır.

Algoritmanın çalışması

Algoritma öncelikle çarpılacak olan sayıları, alt gruplara böler. Örneğin herhangi bir x sayısı aşağıdaki şekilde yazılabilir:

x = x₁B^m + x₀

Buradaki B herhangi bir tabanı ve m bu tabanın herhangi bir üstünü belirtmektedir.

Örneğin 2545 sayısını ele alalım:

2545 = 23 x 10² + 45

Şeklinde yazarsak burada B = 10 ve m = 2 alınmış olur.

Aynı sayı aşağıdaki şekilde de yazılabilir:

2545 = 1 x 5² + 45

Herhangi bir sayı yukarıdaki örneklerde görüldüğü üzere farklı bir taban ve üst değeri kullanılarak yazılabilir.

Kısacası, x sayısı, x₁ ve x₀ olarak iki parçaya bölünmüştür.

Bu algoritmada, çarpımın yapılacağı x ve y sayılarının ikisi de aşağıdaki şekilde parçalanır.

x = x₁B^m + x₀

y = y₁B^m + y₀

Bu parçalama işleminden sonra çarpıma geçilebilir.

xy = (x₁B^m + x₀)(y₁B^m + y₀)

= x₁y₁B^2m + (x₁y₀ + x₀y₁) B^m + x₀y₀

= z₂B^2m + z₁B^m + z₀

Yukarıdaki ilk satırda, çarpımı yapılmak istenen x ve y sayılarının parçalanmış hallerinin çarpımı şeklinde yazılmasını görüyoruz.

Ardından çarpım parantezler içerisine dağıtılıyor ve son olarak çarpım z₂ z₁ z₀ terimler cinsinden yazılıyor. Bu terimleri çekecek olursak:

z₂ = x₁y₁

z₁ = x₁y₀ + x₀y₁

z₀ = x₀y₀

Yukarıdaki z1 terimini açacak olursak aşağıdaki şekilde ilerletmemiz mümkün olur:

z₁ = (x₁y₁ + x₁y₀ + x₀y₁ + x₀y₀) – x₁y₁ – x₀y₀ = x₁y₀ + x₀y₁

Dolayısıyla bir önceki adımda tanımlanan z₂ ve z₀ terimleri ile bu açılım birleştirildiğinde z₁ için aşağıdaki sonuç yazılabilir

z₁ = (x₁ + x₀)(y₁ + y₀) − z₂ − z₀

Örnek

Yukarıdaki çarpma işlemini bir örnek üzerinden göstermeye çalışalım.

Çarpmak istediğimiz sayılar 2543 ve 7532 olsun. Bu sayıları öncelikle parçalıyoruz:

2543 = 25 10² + 43

7532 = 75 10² + 32

Parçalama işlemi ardından sırasıyla çarpma işleminin katsayılarını buluyoruz:

z₂ = 25 × 75 = 1875

z₀ = 43 × 32 = 1376

z₁ = (25 + 43)(75 + 32) − z₂ − z₀ = 68 × 107 − 672 − 2652 = 7276 – 1875 – 1376 = 4025

Yukarıda bulunan katsayıları sonuç denkleminde yerine yazarsak:

z₂ × 10^2×2 + z₁ × 10² + z₀ = 1875 × 10000 + 4025 × 100 + 1376 = 19153876

olarak sonuç doğru bir şekilde bulunur.

Algoritmanın Analizi

Klasik bir çarpma işlemi n haneli iki sayının çarpımı için n2 işlem gerektirir. Yukarıda anlatılan karatsuba algoritması için bu işlem miktarı aşağıda verilmiştir:

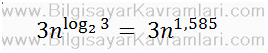
Buradaki n hane için log₂3 çarpma işlemi gerekmesi, yukarıda bulunan her z₂ z₁ z₀ katsayısı için sayının n/2 haneye indirilmesi ve ardından 3 adet çarpma işleminin yapılmasına dayanır.

Bu sayı n<15 için bize klasik çarpmanın daha avantajlı olduğunu gösteriyor. n=15 için yukarıdaki terimin çarpım maliyeti aşağıda hesaplanmıştır:

Görüldüğü üzere klasik yöntemle 15² = 225 değerinden daha az maliyetlidir. Aslında sayının küsuratı sayılmazsa 14 haneli sayılar için neredeyse klasik çarpma ile aynı hızdadır. Dolayısıyla n=14 için iki yöntemin aynı karmaşıklıkta olduğu söylenebilir. Ancak 14’den büyük sayılar için karatsuba çarpımı avantaj sağlayabilmektedir.